[强化学习]AC算法
什么是AC
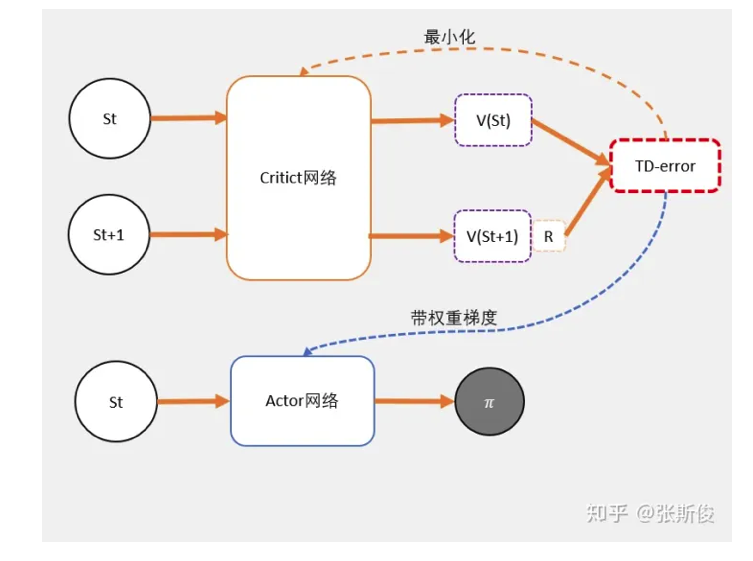
- Actor-Critic使用两个网络。
- 两个网络有一个共同点,输入状态S。
- Actor:输出策略,负责选择动作。
- Critic:计算每个动作的分数。
TD-error
- 在DQN中预估的是Q值,在AC中预估的是V值。
- Q值:评估动作的价值。代表了智能体选择这个动作后,一直到最终状态奖励总和的期望。
V值:评估状态的价值。代表了智能体在这个状态下,一直到最终状态的奖励总和的期望。
Q值和V值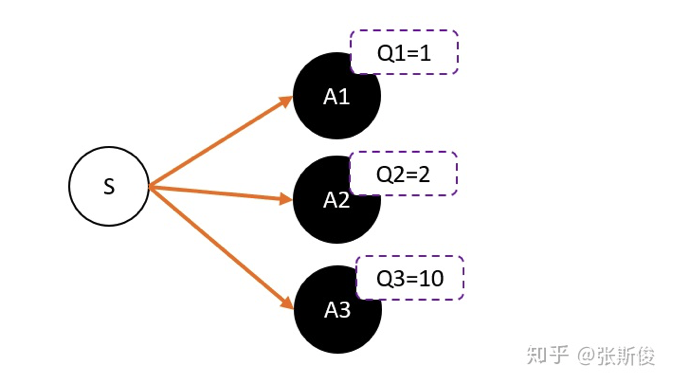
假设我们使用Critic网络,预估到S状态下三个动作A1,A2,A3的Q值分别是1,2,10。
- 但在开始时,我们采用平均策略,随机到A1。于是采用策略梯度的带权重方法更新策略,这里的权重就是Q值。
- 于是策略会更倾向于选择A1,意味着更大概率选择A1。结果A1的概率持续增加。
- 这就掉进了正数陷阱。我们明明希望A3能够获得更多的机会,最后却是A1获得最多的机会。
为什么
- 因为Q值是一个正数,如果权重是一个正数,那么我们相当于提高对应动作的选择的概率。权重越大,调整的幅度也越大。
- 如果我们有足够的迭代次数,就不用担心这个问题的。因为总会有机会抽中到权重更大的动作,因为权重比较大,抽中一次就能提高很高的概率。
- 但在强化学习中,往往没有足够的时间让我们去和环境互动。这就会出现由于运气不好,使得一个很好的动作没有被采样到的情况发生。
- 要解决这个问题,我们可以通过减去一个baseline,令到权重有正有负。而通常这个baseline,我们选取的是权重的平均值。减去平均值之后,值就变成有正有负了。
而Q值的期望(均值)就是V。
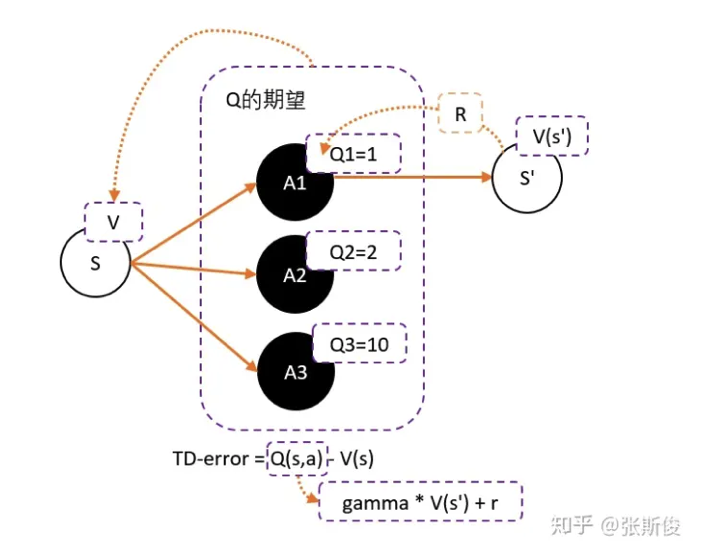
这样我们可以得到更新的权重:$Q(s,a)-V(s).$
- 问题就是我们需要两个网络来估计Q和V。但很多时候,V和Q是可以互相换算的。
- $Q(s,a)$用$\gamma * v(s^{‘})+r$来代替。
- 得到:$TD-error=(\gamma * v(s^{‘})+r) - V(s).$
- 此时的TD-error就是用来更新critic的loss。
- critic的任务就是让TD-error尽量小,然后TD-error给Actor做更新。
总结
- 为了避免正数陷阱,我们希望Actor的更新权重有正有负。因此,我们把Q值减去他们的均值V。有:$Q(s,a)-V(s).$
- 为了避免需要预估V值和Q值,我们希望把Q和V统一;由于$Q(s,a)=\gamma v(s^{‘})+r$。所以我们得到Td-error公式:$TD-error=(\gamma v(s^{‘})+r) - V(s).$
- TD-error就是Actor更新策略时候,带权重更新中的权重值。
- 现在Critic不再需要预估Q,而是预估V。根据马可洛夫链,我们知道TD-error就是Critic网络需要的loss,也就是说,Crtic函数需要最小化TD-error。
算法
- 1.定义两个network:Actor和Critic
- 2.进行N次更新:
- 1.从状态s开始,执行动作a,得到奖励r,进行状态$r^{‘}.$
- 2.记录数据。
- 3.输入到Critic,根据公式:$TD-error=(\gamma * v(s^{‘})+r) - V(s)$求TD-error,并缩小TD-error。
- 4.输入到Actor,计算策略分布。