[强化学习]PG算法
策略梯度(Policy Gradient)
PG是一个蒙特卡洛+神经网络的算法。
蒙特卡洛
步骤
- 我们把智能体放到环境的任意状态;
- 从这个状态开始按照策略进行选择动作,并进入新的状态。
- 重复步骤2,直到最终状态;
- 我们从最终状态开始向前回溯:计算每个状态的G值。
- 重复1-4多次,然后平均每个状态的G值,这就是我们需要求的V值。
原理
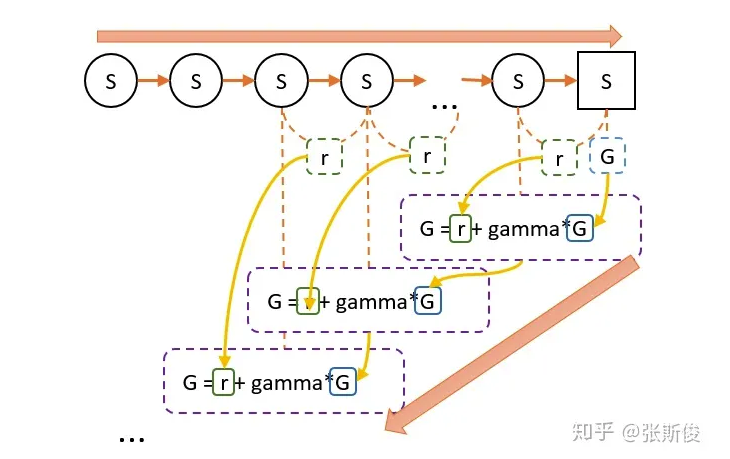
- 第一步,我们跟着策略往前走,一直走到最后,期间只需要记录每一个状态转移和获得的奖励r。
第二步,从终点往前走,一边走一边计算G值。G值等于上一个状态的G值(记为G’),乘以一个折扣率($\gamma$),再加上r。
G值的意义在于,在这一次游戏中,某个状态到嘴中状态的奖励综总和。(理解时可以忽略折扣)。
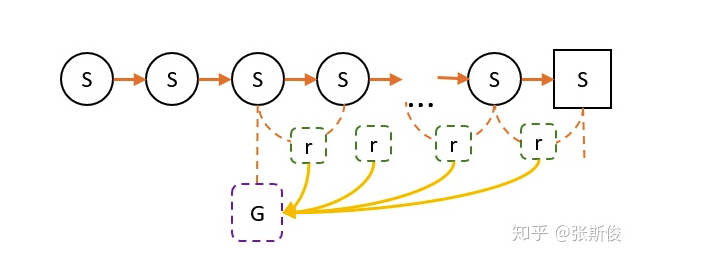
当我们进行多次实验后,可能会经过某个状态多次,也会有多个G值。V值就是所有G值之和的平均值。
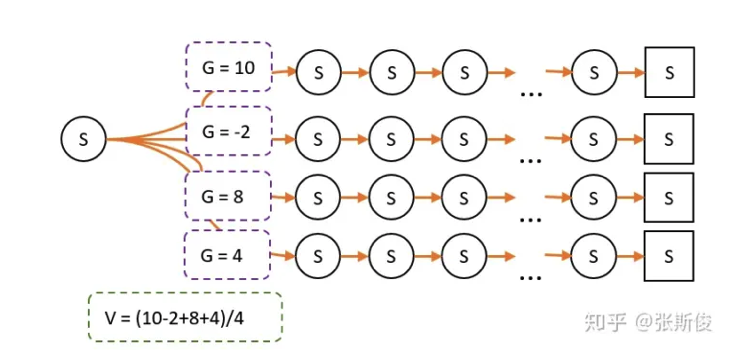
再进一步
- G的意义:在某个路径上,状态S到嘴中状态的总收获。
- V和G的关系:V是G的平局数。
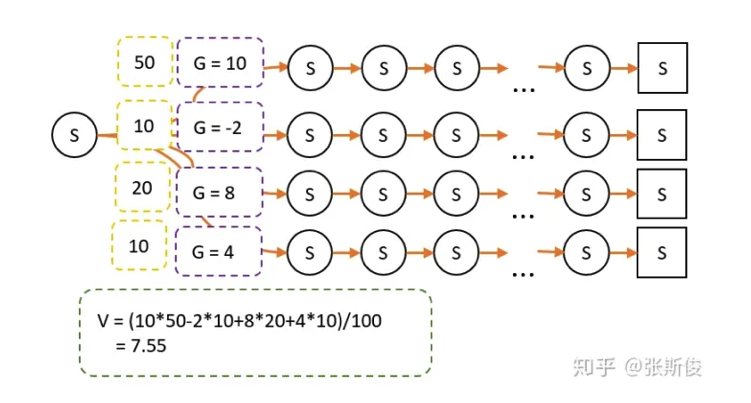
以上图为例,其中有100次经过S点,经过S点后有4条路径到达最终状态,计算G值: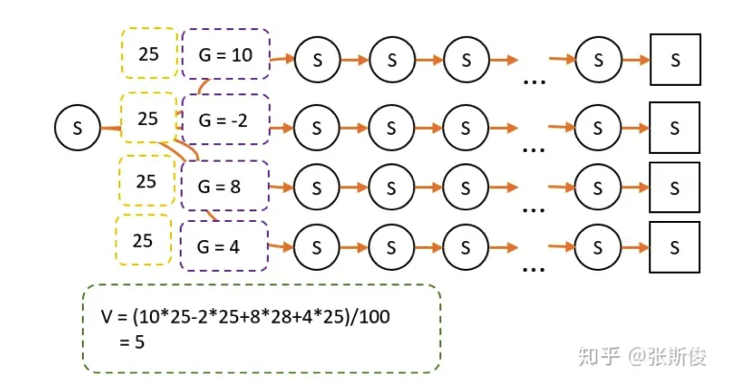
策略A采用平均策略,这时候V=5.
现在采用策略B,由于策略改变,经过某条路径的概率也会发生变化。因此最终试验经过的次数就不一样了。
缺陷
在实际引用中,蒙地卡罗虽然比动态规划消耗要少一点;而且并不需要知道整个环境模型。
但蒙地卡罗有一个比较大的缺点,就是每一次游戏,都需要先从头走到尾,再进行回溯更新。如果最终状态很难达到,那小猴子可能每一次都要转很久很久才能更新一次G值。
PG算法
- 从state出发,可以采取三个动作。
- 假设智能体对这一无所知,那么可能采取平均策略0=[33%,33%,33%]。
- 智能体出发,选择动作A,到达最终状态后开始回溯,得到G=1。
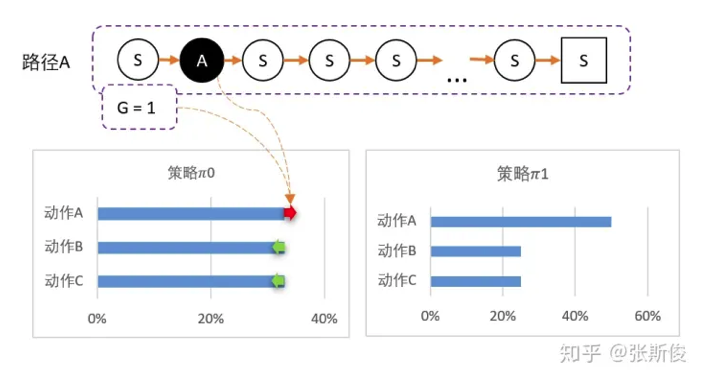
- 我们可以更新策略,因为该路径是选择了A而产生的, 并获得G=1;因此我们需要更新策略:让A的概率提升,相对的,BC的概率降低。得到新策略1=[50%,25%,25%]。
- 虽然B的概率低,但仍有可能被选中。第二轮刚好选中B。
- 智能体选择了B,到达最终状态后回溯,计算得到G=-1.
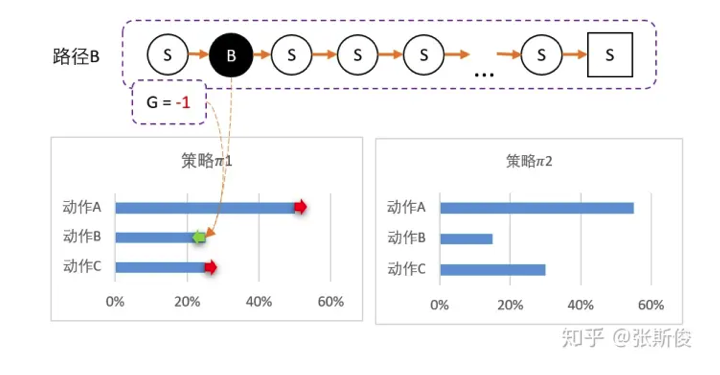
- 所以我们对B动作的评价较低,并且希望以后少选择B,因此降低B选择的概率,相对的,AC的选择将会提高。
- 得到新策略:2=[50%,15%,30%].
- 最后随机到C,回溯计算后,得到G=5.
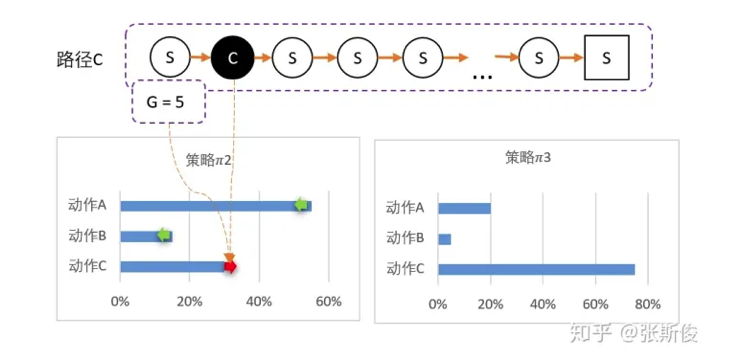
- C比A还要多得多。因此这一次更新,C的概率需要大幅提升,相对地,AB概率降低。 3 = [20%,5%,75%]
当然,以上的例子数值上是不严谨的和精确的。具体怎样调整策略的概率分布,需要更详细的制定。