[算法笔记]粒子群优化(PSO)

发表于 2022-09-20 收录于学习笔记

PSO算法简介

B站视频讲解

算法背景

该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

基础知识

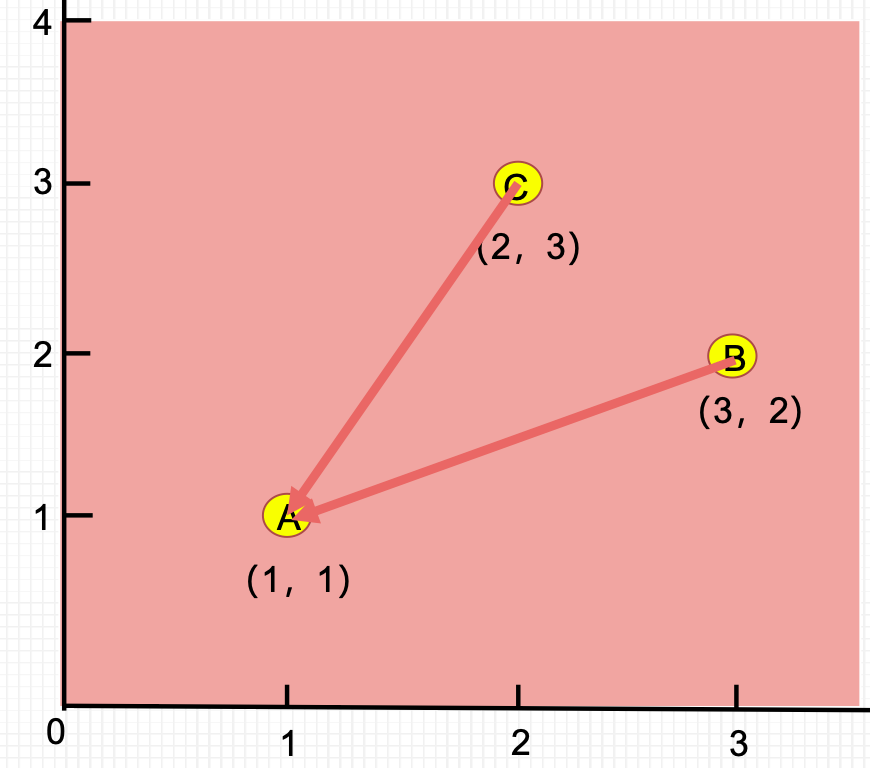
问：已知A为全局最优，B和C如何移动才能到达A处?这个过程如何用数学表达式描述?

某个粒子(点)的移动，是有大小，有方向的。有大小，有方向的东西叫向量。位置就是坐标。
数学的方法:$(1,1)=(2,3)+\alpha \to \alpha = (1,1)-(2,3)=(-1,-2).$
如果A点不一定是个全局最优点，C点在移动到A点的过程中，想要继续探索，可以给其移动的向量加上一个随机值：$(x,y)=(2,3)+rand * (-1,-2).$

算法原理

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量:
$X_{i} = (x_{i 1}, x_{i 2}, . . ., x_{i D}), i = 1, 2, . . ., N$
第i个粒子的“飞行”速度也是一个D维的向量，记为:
$V_{i} = (v_{i 1}, v_{i 2}, . . ., v_{i D}), i = 1, 2, . . ., N$
在第t代的第i个粒子向第t+1代进化时，根据如下式子更新:
$\begin{matrix} v_{i j} (t + 1) = w v_{i j} (t) + c_{1} r_{1} (t) [p_{i j} (t) - x_{i j} (t)] + c_{2} r_{2} (t) [p_{g j} (t) - x_{i j} (t)] \\ x_{i j} (t + 1) = x_{i j} (t) + v_{i j} (t + 1) \end{matrix}$

下一时刻的速度=当前的惯性+个体极值的方向+全局最值的方向

$v_{i j}(t)$代表t时刻粒子的方向，$p_{i j}(t)$代表粒子个体极值的方向， $p_{g j}(t)$代表全局最值。$w,c_1,c_2$代表权重，$r_{1}(t),r_{2}(t)$为随机值。$x_{i j}(t+1)$表示t+1时粒子的位置。

eg.
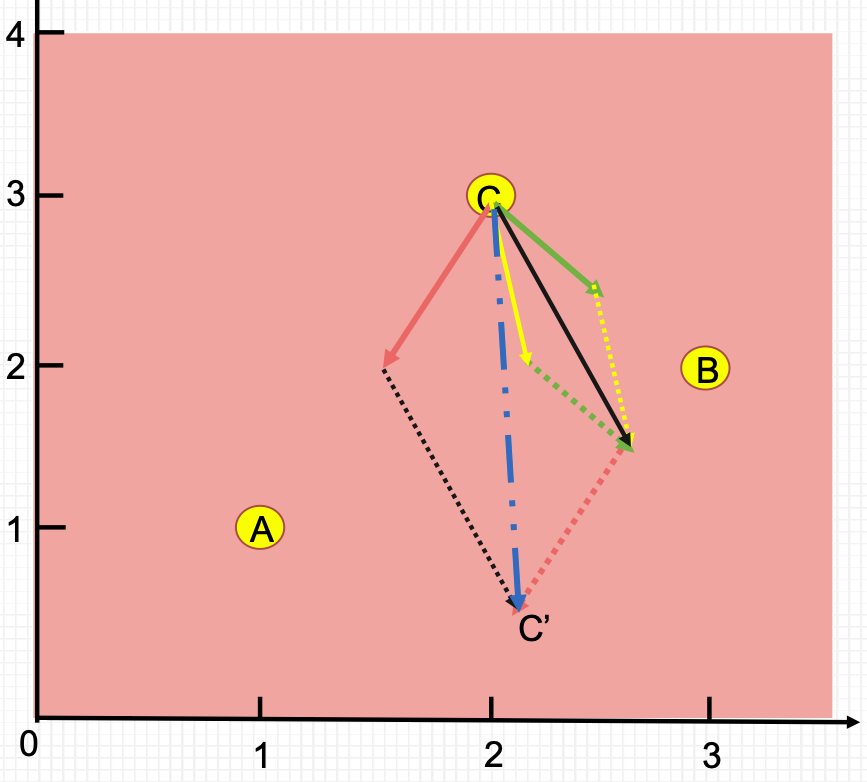
假设某粒子当前位置C，个体极值位置B，全局最优位置A，那么该粒子下一步的运动状态如图所示。

$v_{i j}(t+1)=w v_{i j}(t)+c_{1} r_{1}(t)\left[p_{i j}(t)-x_{i j}(t)\right]+c_{2} r_{2}(t)\left[p_{g j}(t)-x_{i j}(t)\right].$
B对应$p_i$，A对应$p_g$,黄色向量为当前速度方向，绿色向量为向个体极值飞行步长，红色为向全局最值飞行步长。

算法流程

输入：参数$\omega:0.5-0.8,c_1,c_2:0.1-2,v_{max},xß_{max}:$取决于优化函数。
step1:初始化种群$x$;
step2:计算个体适应度*;
step3:更新粒子速度−>更新粒子位置*;
step4:并计算新位置的适应度，若新位置适应度更高，则将该粒子的位置进行更新，否则不更新。
step5:判断是否满足终止条件* ，是则退出，否则返回Step2。
输出：输出最优值。
注：
*1.一般的，我们优化目标是最小化一个函数值。所以个体计算出的函数值越小，适应度越高。
1. max𝑓 = min−𝑓
*2.注意更新速度后，先进行速度边界检测，一般采用$v(v>v_{max}) = v_{max}$ ，位置同理。
*3.常见终止条件为设定迭代进化次数、适应度n代不再变化等。

算法分析

优点：原理比较简单，实现容易，参数少。
缺点：易早熟收敛至局部最优、迭代后期收敛速度慢的。

分析：标准粒子群算法的参数是固定的。𝜔描述的是粒子的“惯性”，在进化前期𝜔应该大一些，保证各个粒子独立飞行充分搜索空间，后期应该小一点，多向其他粒子学习。$c_1,c_2$分别向个体极值和全局极值最大飞行步长。前期$c_1$应该大一些，后期$c_2$应该大一些，这样就能平衡粒子的全局搜索能力和局部搜索能力。3个参数共同影响了粒子的飞行方向，导致即使其他粒子找到更好的，但是当前粒子惯性太大,不能很快的飞向更优的位置。

算法拓展

针对标准PSO的缺点，通常有如下的改进:

1.实现参数的自适应变化。
2.引入一些其他机制，比如随机的因素，速度、位置的边界变化−后期压缩最大速度等。
3.结合其他智能优化算法:遗传算法、免疫算法、模拟退火算法等等，帮助粒子跳出局部最优，改善收敛速度。