[文献阅读]UPOA: A User Preference Based Latency andEnergy Aware Intelligent Offloading Approachfor Cloud-edge Systems UPOA：一种基于用户偏好的延迟和能量感知的云边缘系统智能卸载方法

摘要及其贡献

• 期刊： IEEE Transactions on Cloud Computing.sci-Q2，CCF-C.2022.
• 简称：IMD（互联网移动设备），EN（边缘节点），CD（云数据中心）
• 贡献：
• 可以根据用户偏好来动态调整卸载策略。如用时延换能耗，用能耗换时延。

---

系统模型

用户可以在本地运算，在边缘服务器上运算，在云服务器上运算。

用户偏好的定义

• 定义公式：$U \equiv \lim_{T \to \infty } \frac{1}{T} \sum^T_{t=0}E(\alpha T_{total}(t) + \beta P_{total} (t))$ .

  $T_{total}(t)$表示时隙内的时延，$P_{total} (t)$表示时隙内的能耗。$\alpha,\beta$为权重，$\alpha + \beta = 1$。

• 用户的偏好规则：

  $$\{\begin{array}{l}\alpha >\beta ,{\mathrm{Soc}}_i(t)>{\mathrm{Soc}}^{Up}(t)\\ \alpha =\beta ,{\mathrm{Soc}}^{Down}(t)<{\mathrm{Soc}}_i(t)\le {\mathrm{Soc}}^{Up}(t)\\ \alpha <\beta ,{\mathrm{Soc}}_i(t)\le {\mathrm{Soc}}^{\text{Down }}(t)\end{array}$$

  $Soc^{U p}(t)$表示电池能量状态上限，$ \operatorname{Soc}^{D o w n}(t)$表示电池能量状态下限，低于此标准，用户的将偏向节能。

• eg.

• 电量>$\operatorname{Soc}^{U p}(t)$，则偏向减少时延。

• 电量<$\operatorname{Soc}^{D o w n}(t)$，则偏向减少能耗。
  文中提出了三种偏好规则方案。如下图所示：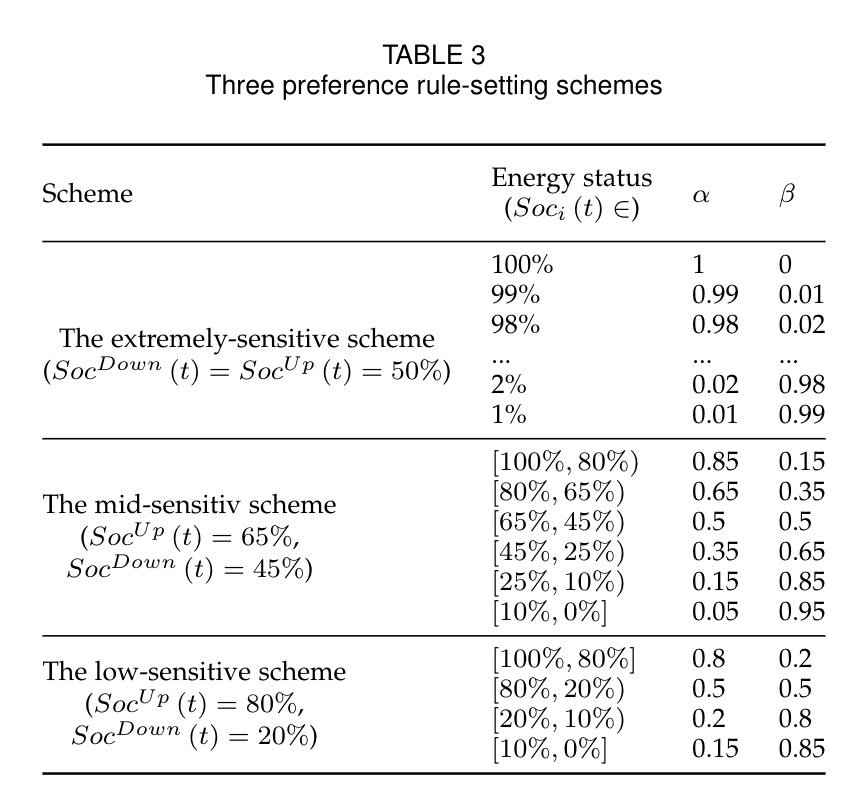
  

• 高敏感方案：$\operatorname{Soc}^{U p}(t)$:50%, $\operatorname{Soc}^{D o w n}(t)$:50%.每当电池减少1%，$\alpha$和$\beta$的值都以0.1的步长进行调整。

• 中等敏感方案：$\operatorname{Soc}^{U p}(t)$:65%, $\operatorname{Soc}^{D o w n}(t)$:35%.设计了六个能量状态区间来调整α和β的值，以平衡能量消耗和延迟。仅当出现电池电量不足警告信息时，低能耗敏感用户才会注意节能。
• 低敏感方案：$\operatorname{Soc}^{U p}(t)$:80%, $\operatorname{Soc}^{D o w n}(t)$:20%.当能量状态小于20%时，β值分别增加到0.75（能量状态为[20%，10%）和0.85（能量状况为[10%，0%]）。

卸载模型

文中提出了五个子模型来表征每个节点在其卸载链路中的任务分配。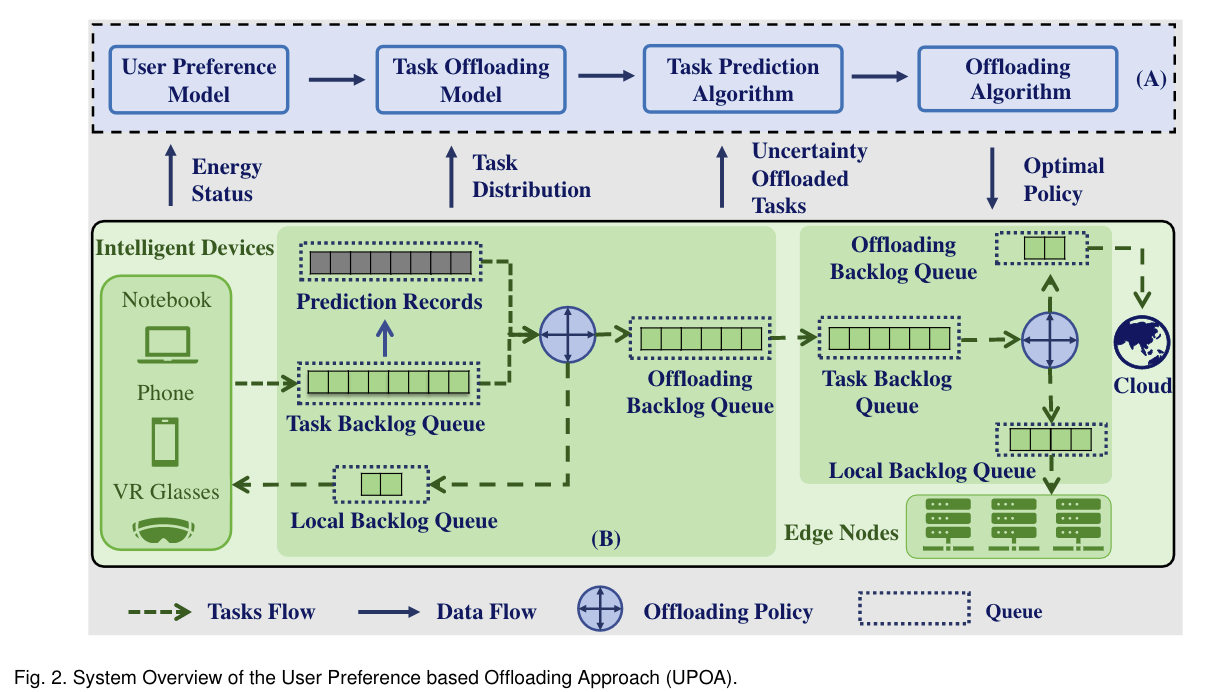

• 预测记录队列(PRQ)：用于预测未来时间窗口内到达的任务数量。每个时隙中，当实际任务到达时，是一任务将替换预测记录队列，为预测算法提供优化反馈。
• 任务积压队列(TBQ)：用于存储等待处理的实时任务。在每个时隙中，TBQ将存储的任分配到本地队列或卸载队列进行处理。
• 本地积压队列(LBQ)：用于存储等待CPU处理的任务。在每个时隙中，LBQ将这些任务发送到CPU进行处理。

• 卸载积压队列(OBQ)：用于存储等待卸载的任务。在每个时隙中，OBQ将这些任务卸载到其卸载目标。任务的传输速率由用户决定。

  因为边缘节点中的任务来自于用户，所以边缘节点不需要PRQ。

时延模型

• 根据little’s 定律，用户的平均等待时间为：$T^i_{av}(t) = \frac{B^i_{imd,q}(t)}{\lambda_i}$

  • $\lambda_i = \mathbb{E}(X_i(t))$,$X_i(t)$为用户i在时隙t内生成的任务。$B^i_{imd,q}(t)$为时隙t内TBQ内的平均任务数量。
  • Little’s 定律：在一个稳定的系统中，长期的平均顾客人数（L），等于长期的有效抵达率（λ），乘以顾客在这个系统中平均的等待时间（W）；或者，我们可以用一个代数式来表达：$L=λW$.

• TBQ可以根据PRQ的预测来提前分发任务。设时隙t和时隙t+k内产生的任务为：$O^i_k(t)$，有：$\sum_{k=0}^K O^i_k(t) = B^i_{imd,q}(t) + B^i_{imd,o}(t)$。

• 传输速率：

  $$\begin{array}{rl}{T}_{\text{tran }}^i(t)& =\varpi {\log }_2(1+\frac{p_{\mathrm{tran},i}(t)s_i}{V{W}_i})\\ 0& <p_{\text{tran,i },i}(t)⩽p_{\text{tran,i }}^{MAX},\mathrm{\forall }i\in N\end{array}$$

• 通过向前滑动窗口来更新PRQ。用户i在时隙t+K时间段生成的任务数量预测表示为：

  $$X(t+k)=\{\begin{array}{l}X(t+k+1),k=K\\ X(t+k+1)-O_k^i(t),1⩽k⩽K-1\end{array}$$

• 再到达时隙t+1时，预测数量$X(t + K +1)$是未知的，用户i的TBQ更新为：$B^i_{imd,q}(t+1)=[B^i_{imd,q}(t)-O^i_t(t)]^++[X(t+1)-O^i_t(t)].$

• 相应的OBQ更新为：$B^i_{imd,o}(t+1) = [B^i_{imd,o}(t) - R^i_imd]^+ +b^i_{imd,o}(t)$.

  $R^i_imd$为要卸载的任务数，$b^i_{imd,o}(t)$为在时隙t内OBQ内到达的任务数量。

• 对于边缘节点，任务的平均等待时延为：$T^j_{av}(t) = \frac{C^j_{en,q}(t)}{\mathbb{E} (\sum_{x \in M_j R^x_{imd}(t)})}$.

  $C^j_{en,q}(t)$为边缘节点TBQ中的任务数量。

• 忽略边缘节点与云的传输延迟。边缘节点的LBQ更新如下：$C^j_{en,q} = [C^j_{en,q} - c^j_{en,q}(t)-c^j_{en,o}(t)]^+ +\sum_{x \in M_j}R^x_{imd}.$

  $ c^j_{en,q}(t)$表示时隙t内边缘节点j中LBQ中的任务分布，$ c^j_{en,o}(t)$表示时隙t内边缘节点j中OBQ中的任务分布。

• 边缘节点j中的OBQ更新：$C^j_{en,o}(t+1) = [C^j_{en,o}(t) - D^j_{en}]^+ + c^j_{en,o}(t).$

• 总时延：$T^i_{total}(t) = \sum_{i \in N}(t^i_{av}(t) + T^i_{tran}(t)) + \sum_{j \in M}T^j_{av}(t).$

  本地等待时延+传输时延+边缘节点的等待时延。

能耗模型

用户的能耗主要由两部分组成：（1）计算能耗。（2）传输能耗。

• $P^i_{total}(t) = \sum_{i \in N} \varpi \vartheta (f_i(t))^3 + \sum_{j \in M} \sum_{i \in M_{imd,j} } \varpi R^i_{imd},$

$\varpi$表示时隙的长度。$\vartheta$表示能耗系数。$R^i_{imd}$表示需要卸载的任务。

任务预测算法

是用LSTM来进行任务预测。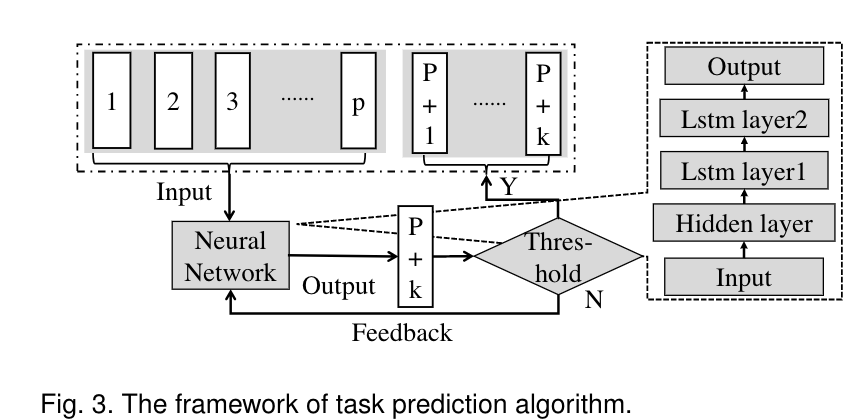

• 输入向量为数据包的大小和时间属性。表示为：$Input_{lstm} = [x^{m_1,t_1}_1,x^{m_2,t_2}_2,…,x^{m_p,t_p}_p].$

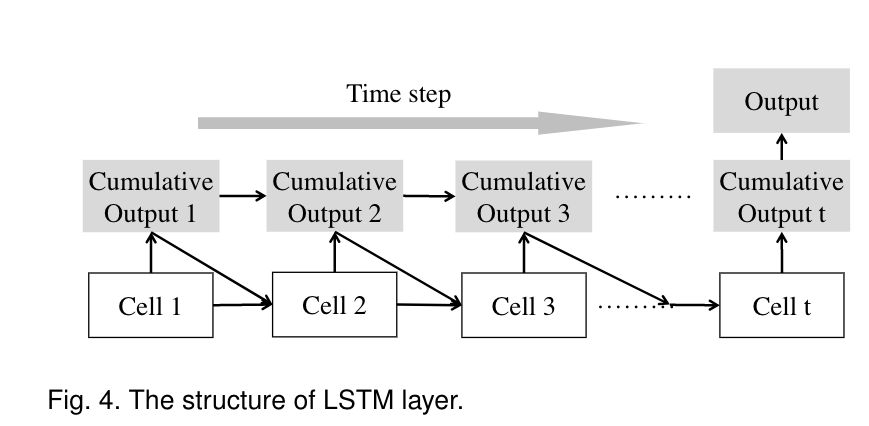
• 包含三层网络：一个隐藏层，两个LSTM层。每个LSTM层的每个时间步生成两个值，一个是当前的输出，一个是之前的累积输出。
  

• LOSS：

  $$\begin{array}{rl}\mathcal{L}(w,u)=& \sum _{v_{x_i}\in V,\widehat{v_{x_i}}\in \hat{V}}{v}_{x_i}{\log }_2(\widehat{v_{x_i}}(w,u)+\xi )\\ & +(1-v_{x_i}){\log }_2(1-\widehat{v_{x_i}}(w,u)+\xi ),\end{array}$$

$\xi = 1 \times 10^{-10}$.$w$为网络参数，$u$为数据包的输入和输出信息。

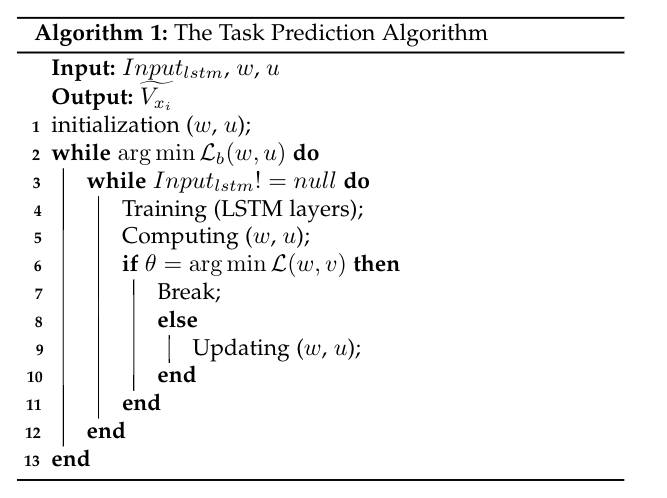
卸载算法

优化问题

将一个任务的数据包转换成向量A： $A=\{a_1,a_2,…,a_Q\}, a_q \in \{0,1\},\forall_q \in \{1,…,Q\}.$

Q表示数据包的数量，$a_q$表示数据包的卸载策略，为0时在本地运算，为1时卸载。

卸载算法设计

基于粒子群优化算法(PSO)。然而，粒子群优化算法正在避免陷入局部最优的趋势。为了解决这个问题，通过添加一个变异算子来开发卸载算法，以防止自身陷入局部最优。

• 目标函数：$F(X)=\sqrt{\frac{F_T^{max} - F_T(x)}{F_T^{max} - F_T^{min}} \cdot \frac{F_P^{max} - F_P(x)}{F_P^{max} - F_P^{min}}}$

$F_T(x)$表示延迟，$F_P(x)$表示能耗。$F_T^{max},F_T^{min}$表示$F_T(x)$的最大最小值。$F_P^{max},F_P^{min}$表示$F_P(x)$的最大最小值。

• 在每个时隙$F(x)=1$表示最优卸载策略，为0则表示策略不可行。目标是让$F(x)$尽可能接近1。

加法运算符

• 让$A^{new}$表示新的卸载策略A。$A^{new}$由旧卸载策略A和粒子速度矢量V来决定(19)：

  $$A^{new}=A+V,a_q^{new}=\{\begin{array}{l}{a}_q,v_q=2\\ v_q,v_q=otherwise\end{array},$$

• V是粒子速度的一维矢量，$V=\{v_1,v_2,…,v_Q\}, v_q \in \{0,1,2\},\forall_q \in \{1,…,Q\}$

$v_i=2$表示粒子i不变。也就是说卸载策略不改变。否则粒子位置将更新为$v_q$

减法运算符

• 粒子的速度可以从粒子位置获得(21)：$$V=A^{new}-A,v_q^{new}=\{\begin{array}{l}2,a_q^{new}=a_q\\ a_q^{new},a_q^{new}=otherwise\end{array},$$

变异算子

由于原粒子群算法收敛速度太快，很容易陷入局部最优。因此添加了一个变异算子，以提高原始PSO的性能。

• $V^M = A \oplus A^{local}$(异或).$A^{local}$是局部最优策略。

• $V^M$中的每个粒子速度$v^M_q$可以表示为(22)：

  $$v_q^M=\{\begin{array}{l}{a}_q^{\text{local }},a_q^{\text{local }}\ne a_q,a_q^{\text{local }}\in A^{\text{local }}\\ 1-a_q^{\text{local }},\text{ otherwise }\end{array}$$

• 判断突变的条件是D小于非常小的数，表示为$D < \theta$。$D = 1- \frac{1}{Q(Q-1)\sum_{i=1}^Q \sum_{j ≠ i}^Q S_{i,j}}.$

D可以理解为每个粒子卸载策略的相似性。

• $S_{i j}=\left|\left\{a_{i q} \mid a_{i q}=a_{j q}, \forall q \in\{1, \cdots Q\}\right\}\right|$.

可以理解为相似性。

例子

• 假设$A = \{1,0,0,1,1\}.$
• 速度$V = \{0,1,1,1,2\}.$
• 根据(19)，新的卸载策略为：$A^{new} = \{0,1,1,1,1\}.$
• 通过$A$和$A^{new}$和(21)可以得到速度$V^{new}=\{0,1,1,2,2\}.$
• 如果$A^{local} = \{1,0,1,0,1\}$,
• 变异操作后的粒子速度为：$V^M=\{0,1,1,0,0\}$.
• 进行加法操作后新的卸载策略为：$A^{new} = {0,1,1,0,0}$.

算法步骤

• step1:确定用户偏好：根据IMD的电池电量状态，根据用户偏好值设置等式1中α和β的权重（参见算法2中的第2行）;
• step2:获得预测结果：任务预测算法（算法1）预测将在未来K时间窗口到达的任务（参见算法2中的第3行）;
• step3:制定卸载策略：
  • 首先随机初始化每个粒子的位置（参见算法2中的第4-9行）;
    • 7:将目前的卸载位置设为历史最佳策略。
  • 执行粒子适应度函数（参见算法2中的第10-19行）。
    • $Gbest_i$：全局最佳策略；
    • $Pbest_i$：历史最佳策略；
    • 10：更新全局策略；
    • 13:计算个体适应度F(x);
    • 14:更新最佳历史策略；
    • 17:更新全局最佳策略；
  • 更新粒子位置（参见Algorithm2中的第20-21行。
  • 判断是否需要调用变异操作（参见算法2中的第22-24行）。

实验模拟

实验环境

文章建立了一个真实的云边缘系统来评估我们的UPOA的性能。使用五部智能手机作为IMD（见表4）。我们设置了两个EN，每个EN都由一个小型工作站组成。该光盘由阿里云上运行的五个配置相同的云节点构建。表5总结了EN和CD的配置。图5为卸载任务的信息。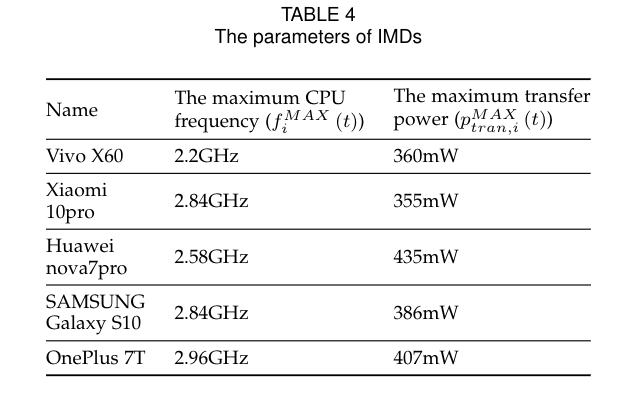

对比算法

• MUDRL(A Multi-update Deep Reinforcement Learning Ap-proach)：优化目标为降低延迟。基于DDQN。2020.
• DRL(A Double-Q Deep Reinforcement Learning Approach):基于DDQN。2020.
• DRL-E2D(A DRL-based Model-free Task Offloading Approach):基于k近邻算法。2021.

模拟结果

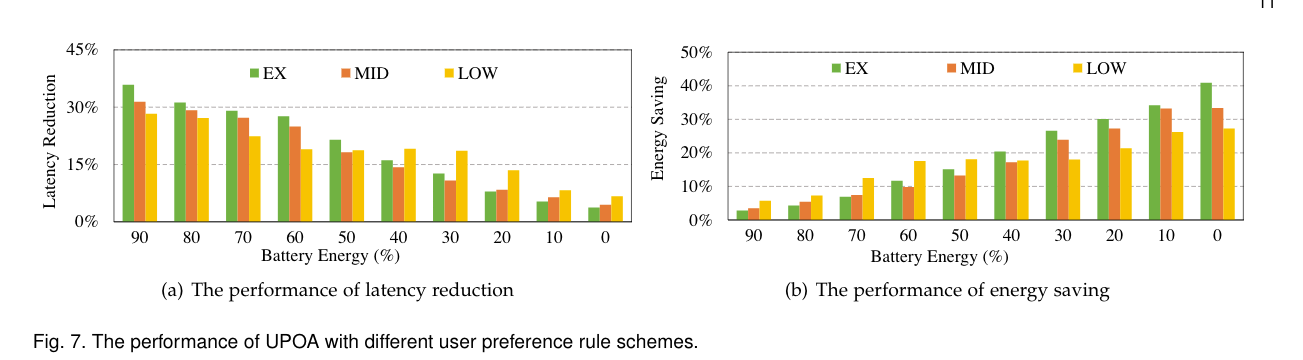
不同偏好对UPOA的影响。

• (a)：能量状态为[100%,50%]时，所有三种方案都会优化延迟，以满足用户对低延迟的需求。其中高敏感方案的延迟最高。
• (b)显示了UPOA在三种不同的方案下的节能性能。(值越高越好)。当能量状态为[100%,50%]时，三种方案的能量优化程度较低。当能源状态为[50%，0%]时，三种方案转向能源优化。结合这两个图的结果，它清楚地表明，当能量消耗到低水平（能量状态为[20%，0%]）时，这三种方案几乎都牺牲了延迟减少，以进一步节能。
• 对于中敏感度方案，当能量状态处于[100%,60%]时，延迟权重为0.85或0.65，为了得到更低的延迟，会把更多的数据包传输到边缘节点，而不是在本地计算。
  
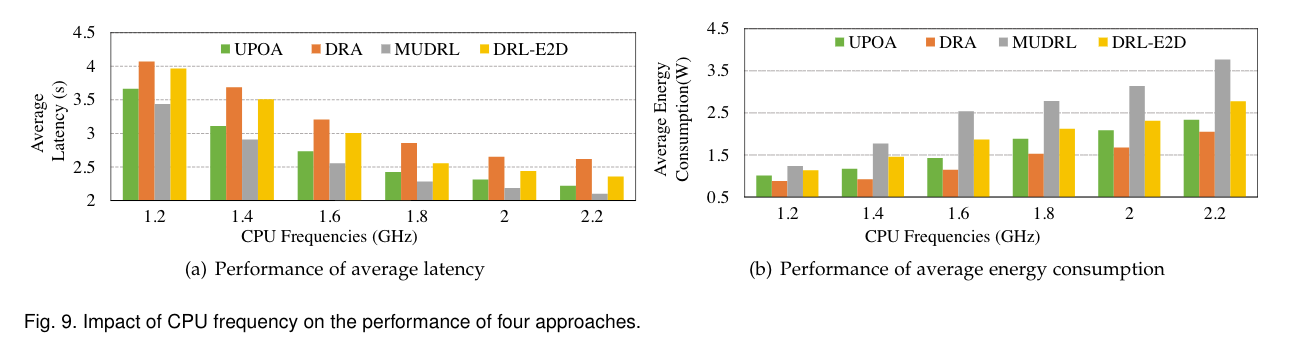
• (a):延迟随着CPU频率的增加而减少。随着CPU频率的增加，可以在本地计算更多的任务，这会减少IMD LBQ中的任务数，从而缩短等待延迟。

• (b):不同CPU频率下四种方法的平均能耗。能源消耗的增加不受传输速度的限制。这是因为如果不对CPU应用节能技术，即使IMD LBQ中的任务很快完成，CPU在等待新任务时也会继续以高频率运行，这会导致更多的能耗。
  

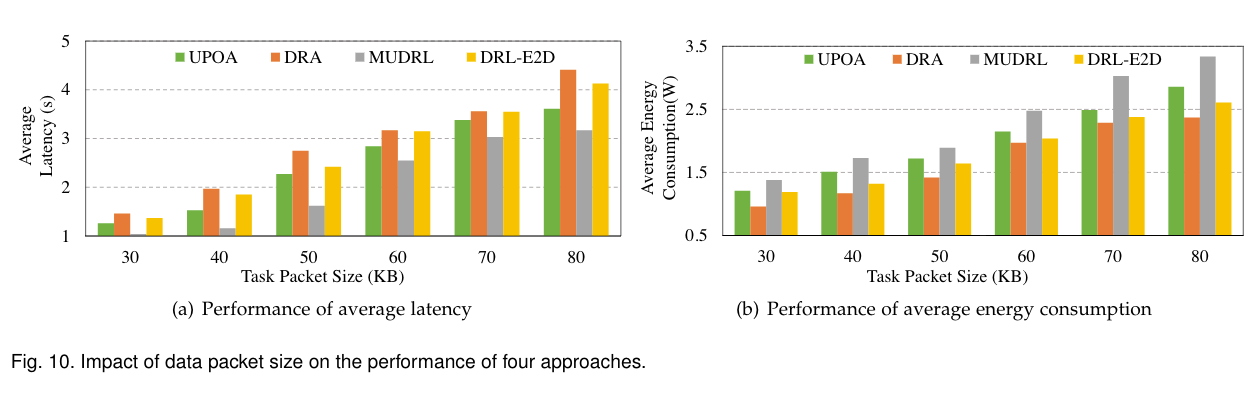
• (a)：平均延迟随着数据包大小的增长而增加。upoa处于DRL-E2D和MUDRL之间。数据包越大，等待延迟越长。卸载的传输时间就越长。

  • DRL-E2D的奖励功能更注重任务的完成率。任务传输时间的增加会降低任务的完成率。奖励功能将优化能量消耗，以获得更好的奖励值，从而增加更多延迟。
  • MUDRL只关注延迟：随着数据包大小的增长，MUDRL会不断增加CPU功率，直到达到最大值。这种机制有效地减少了等待延迟和卸载延迟，但比其他两种方法消耗更多的能量。
  • DRA的奖励功能考虑了任务的最大延迟。因此，当使用DRA方法时，CPU的能耗随着数据包大小的增加而增加。
• (b):能耗随着数据包大小的增长而增加。

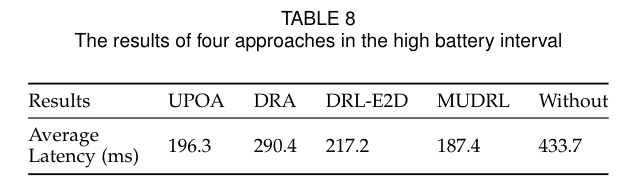
• 在电量充足时的对比，电池电量高的用户更喜欢低延迟。

• 电量低和极地状态下的对比。
  • 可以看到UPOA对能量的保存时最好的。
  • 如果在极低的电池间隔中不卸载方法，电池的平均寿命只有2.6分钟。相比之下，UPOA的平均寿命增加到5.8分钟，额外增加了3.2分钟的时间，这将极低电池间隔的电池寿命延长123.07%。

• 用户设备寿命期间的CPU利用率。每条线上的圆点代表寿命耗尽。
• 可以看出UPOA是最稳定和最低的。

论文地址

Yuan, Jingling, et al. “UPOA: A User Preference Based Latency and Energy Aware Intelligent Offloading Approach for Cloud-edge Systems.” IEEE Transactions on Cloud Computing (2022)