[文献阅读] Deep Reinforcement Learning for CollaborativeOffloading in Heterogeneous Edge Networks 基于深度强化学习的异质边缘网络协同卸载
摘要与贡献
- 会议:CCGrid. 2021
- 贡献:
- 传统的MADDPG算法是非协作的。此算法中Agent可以通过观察它们的本地环境信息并相互协作来以分布式方式学习它们的策略。
- 协作MADRL算法比非合作MADRL算法更健壮,因为即使在多智能体系统中一些智能体发生故障时,协作MADRL算法也能更好地交换信息和更新策略。
系统模型
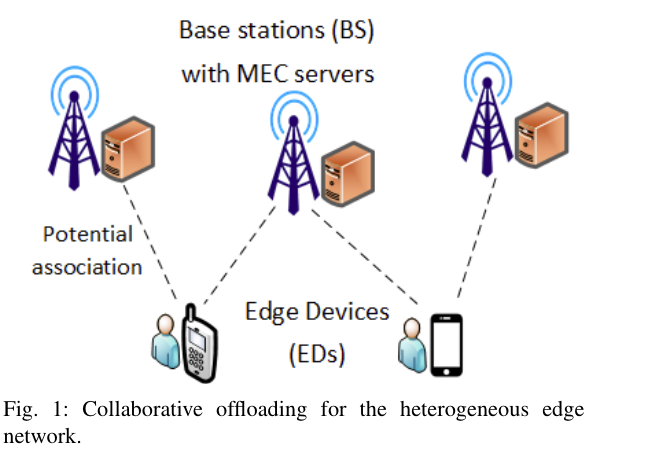
- MEC设备:$\mathcal{M} = \{1,2,…,M\}$.
- 用户设备:$\mathcal{N} = \{1,2,…,N\}$.
- 每个用户设备都一个任务要处理。任务$Y_n=(C_n,D_n,T_n^{max})$,$C_n$:总共需要的计算资源,$D_n$:任务大小,$T_n^{max}$:任务允许的最大延迟。
传输模型
- 定义$\mathcal{K} = \{1,2,..,K\}$为每个MEC设备的可用子集集合。
- 二分变量:$x_{n,m}^k \in \{0,1\}$。1:在MEC,0:在本地计算。
- 卸载策略:$\mathcal{x} = \{x_{n,m}^k|x_{n,m}^k=1, n \in \mathcal{N}, m \in \mathcal{M}, k \in \mathcal{K}\}$。包含了所有任务卸载变量。
- 定义$\mathcal{N}_n = \{n \in \mathcal{N}|\sum_{k \in \mathcal{k}x_{n,m}^k=1,}\}$表示为将其任务卸载到MECm用户集合。
- 传输能耗:$\mathcal{P} = \{p_n^k| 0 < p_n^k ≤P_n^k,n \in \mathcal{N} \}$,$p_n^k$为用户卸载任务$Y_n^k$所需的能耗。
- 传输速率:
W为带宽,$\sigma^{2}$为噪声。
传输时间:$T_n^{up}=\sum_{m \in \mathcal{M}} \frac{D_n}{R_{n,m}},\forall n \in \mathcal{N}$.
能耗:$E_n^{up}=p_nT_n^{up}=p_n\sum_{m \in \mathcal{M}} \frac{D_n}{R_{n,m}},\forall n \in \mathcal{N}$,
$p_n=\sum_{k \in \mathcal{k}}p_n^k \forall n \in \mathcal{N}$
计算模型
本地计算
- 时间:$T_n^l = \frac{D_n}{f_n^l}$.
- $E_n^l=k(f_n^l)^2C_n$.
k:能耗系数。$f_n^l$本地计算能力。
MEC服务器
- 计算时间:$T_n^{ex} = \sum_{m \in \mathcal{M}} \frac{C_n}{f_m^e} ,\forall n \in \mathcal{N}$.
- 总时间:$T_n^{off} = T_n^{up} + T_n^{ex} = \sum_{m \in \mathcal{M}}(\frac{D_n}{R_{n,m}} + \frac{C_n}{f_m^e}),\forall n \in \mathcal{N}$
- 能耗:$E_n^{off} = E_n^{up} = p_n\sum_{m \in \mathcal{M}}\frac{D_n}{R_{n,m}}, \forall n \in \mathcal{N}$.
优化目标
- 总时间:$T_{n}=T_{n}^{o f f} \sum_{m \in \mathcal{ßM}} x_{n m}+T_{n}^{l} \sum_{m \in \mathcal{M}}\left(1-x_{n m}\right), \forall n \in \mathcal{N}$
- 总能耗:$E_{n}=E_{n}^{o f f} \sum_{n \in \mathcal{M}} x_{nm} +E_{n}^{l} \sum_{n \in \mathcal{M}}\left(1-x_{n m}\right), \forall n \in \mathcal{N}$
- 优化目标:$J_n = \lambda_n^T(\frac{T^l_n - T_n}{T^l_n}) + \lambda_n^E(\frac{E^l_n - E_n}{E^l_n})$。
- (本地时间-总时间)/总时间 + (本地能耗-总能耗)/总能耗
- $\lambda_n^T, \lambda_n^E \in [0,1] ,(\lambda_n^T + \lambda_n^E = 1)$。这两个参数由用户设备设置,如果任务紧急可以增加时间消耗的权重。如果用户设备电池电量低,则优先考虑能耗因素。
如果任务在本地计算,$J_n=0$。如果卸载模式的时间和能耗低于本地计算的则$J_n >0$。目标为最大化$J_n$
给定卸载策略$\mathcal{X}$,能耗策略$\mathcal{P}$,优化问题为:
(C1)和(C2)意味着每个任务可以在本地执行或卸载到一个子通道上的至多一个MEC服务器。(C3)表示每个ED的发射功率约束。约束(C4)确保每个任务必须在延迟约束下完成。
MDP
State
- $\mathcal{S}(t)= \{S_{task}(t),S_{channel}(t),S_{power}(t)\}$.
- $S_{task}(t)=[D_n(t), C_n(t)].$
$S_{channel}(t) = c_n^k(t) = \begin{bmatrix}
c_{1,1}& … & c_{1,k}\\
.& . & .\\
. & . & .\\
. & . &. \\
c_{N,1}& … &c_{N,K} \\
\end{bmatrix}
$$c_n^k(t)$表示是否使用子信道。是为1,否为0.
$S_{power}(t) = p_n^k(t) = \begin{bmatrix}
p_{1,1}& … & p_{1,k}\\
.& . & .\\
. & . & .\\
. & . &. \\
p_{N,1}& … &p_{N,K} \\
\end{bmatrix}
$$p_n^k(t)$表示传输功率。
Action
- 卸载决策:$x_{nm}^t(t)\in\{0,1\}$.
- 选择信道:$k(t)=[1,2,…,K]$.
- 传输功率:$p_n^K\in(0,O_n^k]$
Reward
- $r(s(t),a(t))=\sum_{n \in \mathcal{N}}r(s_n(t),a_n(t))=J(t)$.
算法模型
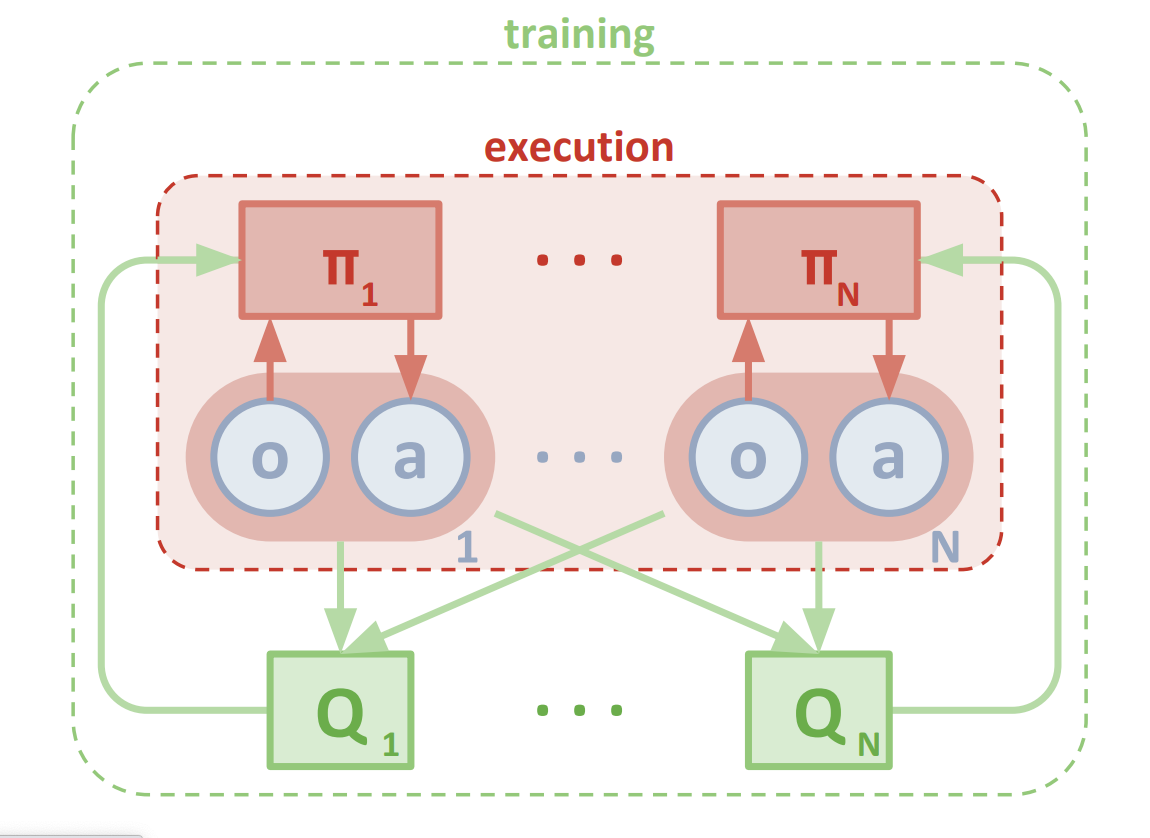
MADDPG模型

算法
- 作者提出的MA-DDPG算法基于MADDPG。
- agent策略表示:$π=\{π_1,π_2,..,π_N\}$,策略网络参数:$\theta=\{\theta_1,\theta_2,..,\theta_N\}$.
- agent更新他们自己的参数以获得最优策略 $π_{\theta_n}^{*}=argmax_{\theta_n}J(\theta)$,$J(\theta)$是一个目标函数。
- actor网络梯度:$\nabla_{\theta_{n}} J\left(\pi_{n}\right)=\mathbb{E}_{\mathbf{0}, a \sim \mathcal{D}}\left[\nabla_{\theta_{n}} Q_{n}^{\pi}\left(\mathbf{0}, a_{1}, \ldots, a_{N}\right) . \nabla_{\theta_{n}} \pi_{n}\left(a_{n} \mid o_{n}\right)\right]$。
- critic网络更新:$L\left(\theta_{n}\right) =\mathbb{E}_{\mathbf{0}, a, r, \mathbf{o}^{\prime}}\left[\left(y_{n}-Q_{n}^{\pi}\left(\mathbf{o}, a_{1}, a_{2}, \ldots, a_{N}\right)\right)^{2}\right]$.
$ y_{n} =r_{n}+\left.\gamma Q_{n}^{\pi}\left(\mathbf{o}^{\prime}, a_{1}^{\prime}, a_{2}^{\prime}, \ldots a_{N}^{\prime}\right)\right|_{a_{n}^{\prime}=\pi_{n}^{\prime}\left(o_{n}\right)}$
总结
个人感觉只是将MADDPG算法运用到了这个系统上,创新性不高。