[文献阅读] Optimal Computation Offloading in CollaborativeLEO-IoT Enabled MEC: A Multi-agent DeepReinforcement Learning Approach 支持协同LEO-IoT的MEC:一种多智能体深度强化学习方法
摘要及贡献
- 期刊:IEEE Transactions on Green Communications and Networking SCi- Q1
- 主要贡献:
- 将优化问题转化为POMDP问题,提出了一种基于DRL的求解算法MAIBJ。通过在MAIBJ中设计的判决器结构,卫星可以有效地与其他卫星进行联合资源分配。
系统模型
传输模型
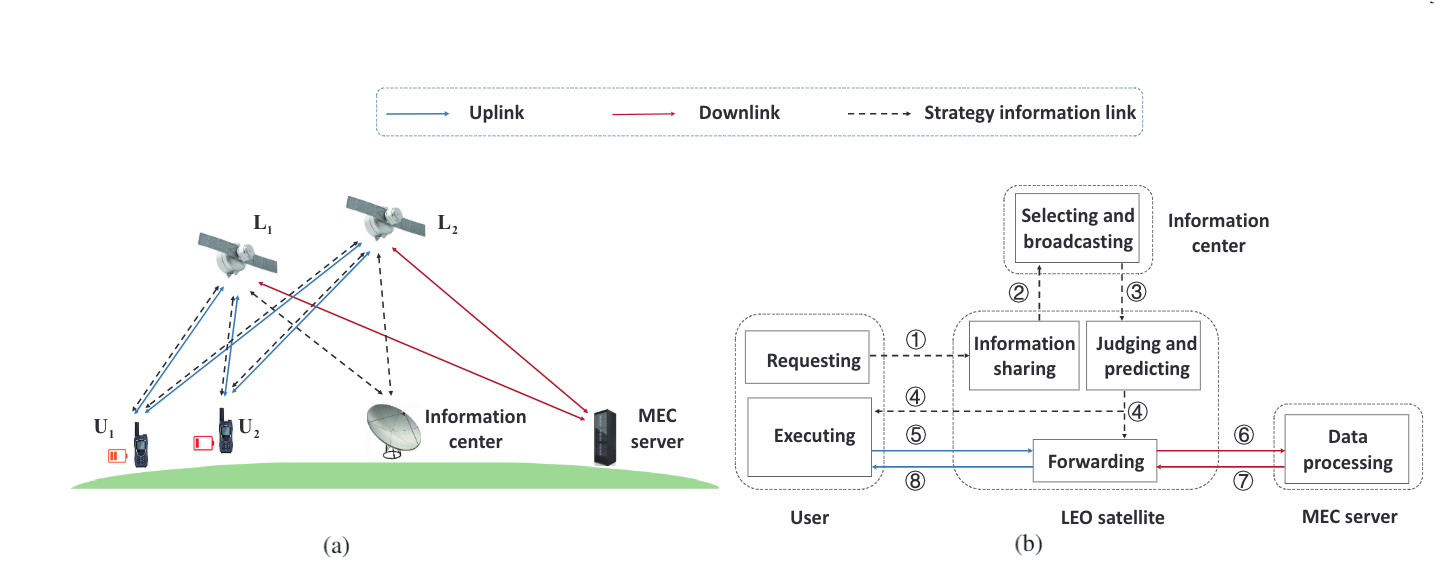
(a) LEO-IoT的体系结构
(b) 架构内的工作流:① 用户向LEO卫星请求链路资源分配;② LEO卫星将接收到的用户信息雨信息中心共享;③ 信息中心选择并向LEO卫星广播信息;④ LEO卫星为用户和自己分配资源,并对用户做出响应; ⑤ 用户按照卫星的资源分配策略上传任务到LEO;⑥ 数据由LEO卫星转发到MEC进行处理;⑦-⑧ 结果通过LEO卫星返回到用户。
- 如图所示,采用LEO作为用户和MEC之间的信息桥梁。
- 我们假设每个用户的计算任务通过LEO卫星卸载到唯一的MEC服务器,而无需本地处理。处理数据后,MEC服务器将结果返回给用户。
- 假设有N个用户,用户 $i$ 定义为 $U_i$ ,集合表示为 $\mathcal{U}=\{U_i|i=1,…,N\}$ .
- 有M颗LEO卫星,只有一个MEC服务器。卫星 $j$ 定义为 $L_j$ ,集合表示为 $\mathcal{L}=\{L_j|j=1,…,M\}$ .
- 总时间周期T被分为W个时隙,每个时隙为 $\tau$ ,$\tau = T/W$ .
数据在每个时隙由不同的卫星以不同的传输速率转发。上行/下行链路的速率是不同的,上行链路的发射功率由用户提供,下行链路的发射功率由卫星提供。假设卫星工作在Ka波段,上行链路和下行链路的中心频率为20GHz。
- 上行链路根据任务大小分配,下行链路功率固定,为卫星的最大功率 $P_L$。
- 用户$i(U_i)$到卫星$j(L_j)$的上行链路带宽和发射功率为 $B^t_{i,j},P^t_{i,j}$ ,LEO卫星$L_j$到MEC服务器的带宽为 $B_j^t$ 功率为 $P_L$
由于每颗卫星都只拥有用户上传的信息,而不了解其他卫星的策略,在这种情况下很难分配电力。因此作者设计了一个陆地信息中心,在那里使用神经网络将卫星上传的信息广播给其他卫星作为补充。并设计了一种判决器结构,其中每颗卫星都实现了神经网络,以确定是否利用接收到的信息来提高决策的灵活性。 广播信息只是卫星的补充数据,而不是实际的卸载数据。与数据卸载相比,信息传输的延迟和能量消耗可以忽略不计。
- 在时间T中,LEO沿着自己的轨道飞行。在时隙t内,$U_i$和$L_i$的仰角表示为$\theta_{i,j}^t$。类似的,与MEC之间的仰角为$\theta_j^t$。
- 从$U_i$到$L_j$的上行速率 $g^y_{i,j}$ 以及从$L_j$到MEC的下行速率 $g^y_j$ 为:
$g^y_{i,j} = G_T + G_R - [32.45 + 20 \times log_{10}(D_{i,j}^t \times f_c)]$ $g^y_j = G_T + G_R - [32.45 + 20 \times log_{10}(D_j^t \times f_c)]$
$G_T$为发射天线增益,$G_R$为用户和卫星接收天线增益。$D_{i,j}^t$和$D_j^t$为$U_i$到$L_j$和$L_j$到MEC服务器的距离(单位为km)。$f_c$是中心载频,单位为[mHZ],Ka频段为20000兆赫,不考虑链路之间的带宽差异。$32.45 + 20 \times log_{10}(D_{i,j}^t \times f_c)$和$32.45 + 20 \times log_{10}(D_j^t \times f_c)$为上行/下行链路的空闲空间损失,不考虑其他衰减。
- 信噪比(SNR)为:
$SNR_{i, j}^{t} =\frac{P_{i, j}^{t} \times g_{i, j}^{t}}{N_{0} \times B_{i, j}^{t}}$ $SNR_{j}^{t} =\frac{P_{L} \times g_{j}^{t}}{N_{0} \times B_{j}^{t}}$
$N_0$是噪声密度(AWGN).$N_{0} \times B_{i,j}^{t}$和$N_{0} \times B_{j}^{t}$为高斯白噪声功率。
- 传输速率为:
$C_{i,j}^t = B_{i,j}^t \times log_2(1 + SNR_{i,j}^t)$ $C_{j}^t = B_{j}^t \times log_2(1 + SNR_j^t)$
优化目标
- 目标:以较低的能耗快速卸载数据。
- 假设在时隙t中用户$U_i$有$V_i^t$大小的任务要传输。下一个时隙的任务量为:
$V_{i}^{t+1}=V_{i}^{t}-\sum_{j=1}^{M} C_{i, j}^{t} \times \min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right)$
$\sum_{j=1}^MC^t_{i,j}$是在时隙$\tau$内用户$U_i$到卫星的上传速率之和。$\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right)$表示每个时隙内的实际传输时间。如果任务$V_i^t$没有在时隙内完成,那么整个时隙都会被用于计算,且$\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}} > \tau$,该时隙的传输延迟为$\tau$。相对的,如果$V_i^t$完成了,那么$\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}} < \tau$,传输延迟为$\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}$。
基于此模型,我们将优化问题表示如下:
\begin{array}{l} \text { (P1) } \min _{B_{i, j}^{t}, B_{j}^{t}, P_{i, j}^{t}}\left\{\sum_{t=1}^{W} \sum_{i=1}^{N} \min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right)+\beta \times\right.\\ \left.\left[\sum_{t=1}^{W} \sum_{i=1}^{N}\left(\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right) \times \sum_{j=1}^{M} P_{i, j}^{t}\right)+\sum_{t=1}^{W} \sum_{j=1}^{M} t_{\max } \times P_{L}\right]\right\}\\ \text { s.t. } \quad \sum_{j=1}^{M} P_{i, j}^{t} \leq P_{U}, i=1, \ldots, N \text {, }\\ \sum_{i=1}^{N} B_{i, j}^{t}+B_{j}^{t}=B^{t o t}, j=1, \ldots, M\\ \sum_{i=1}^{N} C_{i, j}^{t} \leq C_{j}^{t}, j=1, \ldots, M\\ \theta_{i, j}^{t} \geq \theta_{m}, i=1, \ldots, N, j=1, \ldots, M \text {, }\\ \theta_{j}^{t} \geq \theta_{m}, j=1, \ldots, M \text {. } \end{array} $\sum_{t=1}^{W} \sum_{i=1}^{N} \min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right)$是所有用户的累积传输延迟。如果$V_i=0$那么$\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right) =0$。
- 优化目标为最小化整个时间T内的网络延迟。
- 同时,所有LEO卫星在T时间内的传输能耗也应该被最小化。
- $\sum_{t=1}^{W} \sum_{i=1}^{N}\left(\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right) \times \sum_{j=1}^{M} P_{i, j}^{t}\right)$表示时间T内的LEO卫星的所有能耗。
- 我们定义时隙t内$t_{max}$为最大传输时间,$t_{max}$为$\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right)$的最大值。
- 如果仍然有数据要卸载,可以利用卫星转发到MEC服务器。因此。$\sum_{t=1}^{W} \sum_{j=1}^{M} t_{\max } \times P_{L}$表示所有LEO卫星的能耗。
- $\beta$为权重,$\beta>0$。
- 目标为分配$B_{i,j}^t,B_{j}^t,P_{i,j}^t$,最小化延迟和能耗消耗的加权和。
强化学习模型
将优化问题转化成POMDP问题。
Agent
- 每个LEO卫星$L_j$都是一个Anget,为自身的上行/下行链路分配带宽和资源。但是,每个用户都必须满足(8)的约束,因此,每个agent都应该根据协作机制共同协作来分配资源。
Observation
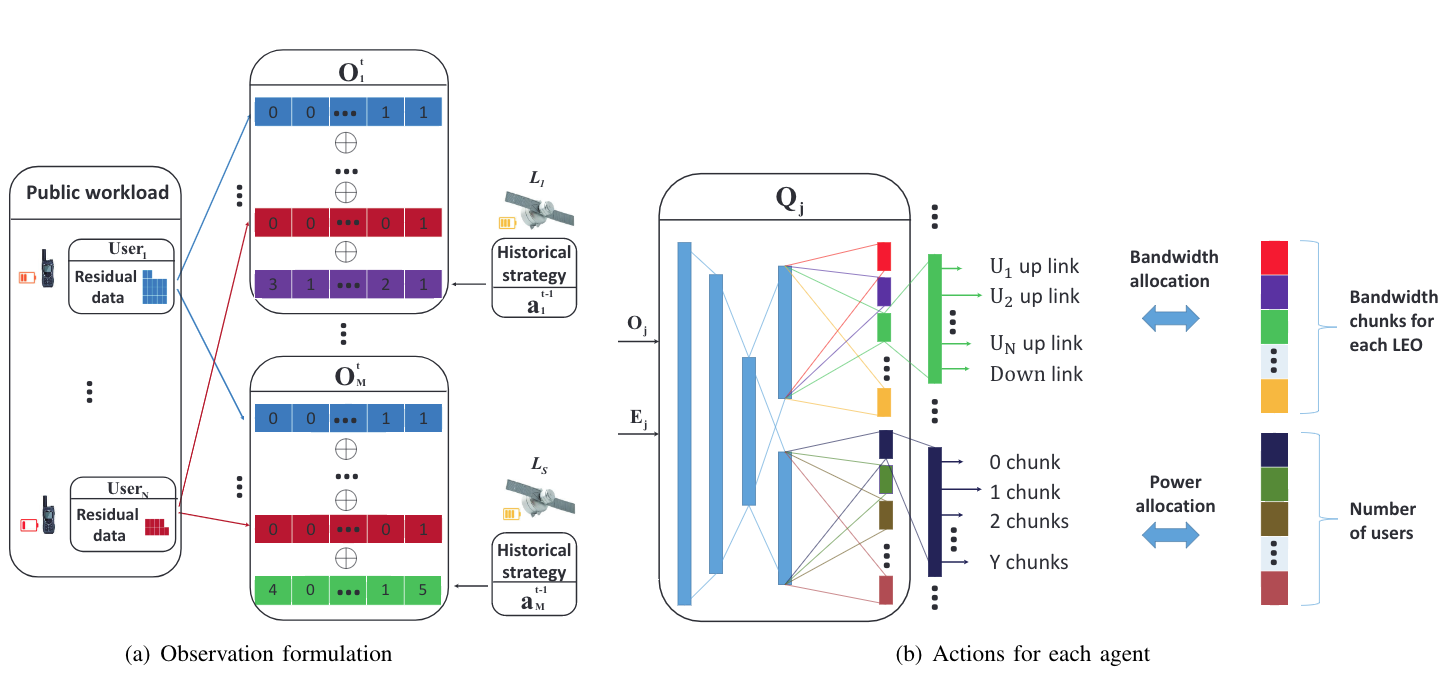
- 如图2(a)所示,j的$O_j^t$由几个公共的二进制向量(蓝色和红色)和一个局部的二进向量(紫色和绿色)组成。
- 公共二进制向量是每个用户的剩余数据,向量的长度是由数据量决定的。
- 局部向量时隙t-1的动作空间向量$a_j^{t-1}$。
Action
- 如图2(b)所示,分为带宽矢量和功率向量。
- 带宽向量为每个Agent所确定的所有相关双链路和下行链路所使用的频率资源。
- $L_j$的可用资源$B^tot$划分为C份,每块的频率定义为$B^c$,$B^c=B^tot/C$ 。
- 每个区块将仅分配给N+1链接中的一个。因此带宽向量的长度为C(颜色从红色到黄色)。对于每个向量中的元素,有N+1个之可以选择(N个上行链路 + 1个下行),定义为$\{,1,2,…,N,N+1\}$.
- 每个Agent的带宽向量表示特点带宽被分配到哪条链路。
- 对于功率资源,每个Agent必须确定所有相关的上行链路功率,下行链路功率是固定的。
- 将每个用户的最大发射功率$P_u$划分为Y块。
- 在图2(b)中,功率向量的长度为N(从蓝色到粉色),每个Agent必须为所有上行链路分配资源。
- 有Y+1个可能的值(Y个功率块 + 1个0功率),每个之代表对应上行链路的其中一个功率块。记为$\{1,2,…,Y,Y+1\}。
Reward
在T时间内t时隙内的延迟表示为:
$r_L^t = \sum_{i=1}^N min(\frac{V_i^t}{\sum_{j=1}^MC^t_{i,j}}, \tau)$ 所有用户在T时间内t时隙中的能耗表示为:
$r_{E U}^{t}=\sum_{i=1}^{N}\left[\min \left(\frac{V_{i}^{t}}{\sum_{j=1}^{M} C_{i, j}^{t}}, \tau\right) \times \sum_{j=1}^{M} P_{i, j}^{t}\right]$ 所有LEO卫星的能耗表示为:
$r_{EL}^t = \sum_{j=1}^M t_{max} \times P_L$
其中$t_{max}≤\tau$
总能耗:
$r^t_E=r^t_{EU}+r^t_{EL}$ 为了满足(8)的约束,加入一个惩罚$r^t_{C1}$。如果每个用户的能耗超过了$P_U$:
$r_{C1}^t=\sum_{i=1}^N(\sum_{j=1}^M P_{i,j}^t - P_U)$ 为了满足(10)的约束,加入一个惩罚$r^t_{C3}$。如果每个LEO卫星上行速率大于下行速率:
$r_{C3}^t=\sum_{j=1}^M(\sum_{i=1}^N C_{i,j}^t - C_j^t)$ 总惩罚:
$r_C^t = r_{C1}^t +r_{C3}^t$ reward:
$r^t =-(r_L^t + \beta \times r_E^t + \lambda \times r_C^t)$
其中β为调整优化函数(P1)的系数,λ为满足约束条件的系数,β=0.1,λ= 0.1。
MAIBJ
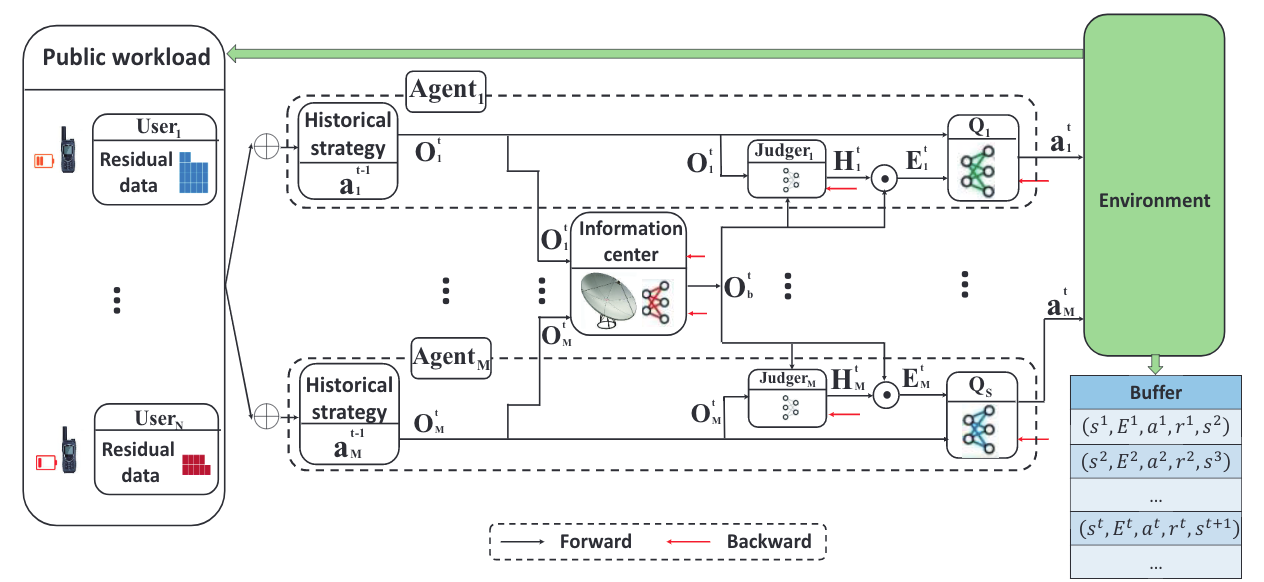
- 如图所示。信息中心部署有一个神经网络来选择要广播的信息。每个Agent都有一个判断网络和一个Q网络。
- 每个时隙t中,Agent都会获得一个$O_j^t$并上传到信息中心。
- 信息中心选择一个$O_b^t$并将其广播给其他Agent。
- 每个Agent的判断网络收到信息后,决定是否接受。每个Q网络根据局部观察和接收到的信息分配资源。
- 采取一个action,获得一个全局奖励$r^t$,进入下一个state$s^{t+1}$。
网络
信息中心网络:
- $Input:\{O_1^t,O_2^t,…,O_M^t\} \to Output:\{O_b^t\}$ .
- $b \in \{1,2,..,M\}$
- 使用sofmax函数归一化,概率选择。
判断网络:
- $Input:\{O_j^t,O_b^t\} \to Output:\{H_j^t\}$
- $E_j^t = H_j^t \odot O_b^t$.如果$E_j^t$为1,代表接受此信息。0为拒绝。
- 64 x 32 x 2。最后一层为2,即两点分布。
Q Network:
- $Input:\{O_j^t,E_j^t\} \to Output:\{a_j^t\}$
- 前3层神经元分别为512个、256个和128个。
- 最后一层分为带宽和功率。
- 带宽:有C个子网络,每个子网络有N+1个神经元。
- 功率:有N个子网络,每个子网络有Y+1个神经元。
训练
Q Network:
- 基于DQN。
- Loss Function:$\mathcal{L}^{Q}\left(\theta_{Q}\right)=\frac{1}{B_{m}} \sum \frac{1}{S} \sum^{M}\left(y_{i}-Q\left(O_{j}^{t}, E_{j}^{t}, a_{j}^{t} ; \theta_{Q}\right)\right)^{2}$
- $\theta_Q$是网络参数
- $y_i=\left\{\begin{array}{ll}
r^{t}, & \text { if episode terminates at } \mathrm{t}+1 \\
r^{t}+\gamma \cdot \max _{a_{j} t+1} Q\left(O_{j}^{t+1}, E_{j}^{t+1}, a_{j}{ }^{t+1} ; \hat{\theta}_{Q}\right), \text { otherwise. }
\end{array}\right.$ - $\hat{\theta}_Q = \alpha \cdot \theta_Q + (1 - \alpha) \cdot \hat{\theta}_Q$
判断网络:
- 利用Actor-Critic网络。
- 每个判断的两点分布式为Actor,对应的Q值被认为是Critic。
- 每个判断网络的参数为$\theta_j$。
- Loss Function:$\begin{aligned}
\nabla_{\theta_{J}} J\left(\theta_{J}\right)=& E_{O_{j}^{t}, O_{b}^{t} \sim \rho^{\pi_{O}}, H_{j}^{t} \sim \pi_{\theta_{J}}}\left[\nabla_{\theta_{J}} \log \pi\left(H_{j}^{t} \mid O_{j}^{t}, O_{b}^{t}\right)\right.\\
&\left.\cdot Q\left(O_{j}^{t}, E_{j}^{t}, a_{j}^{t} ; \theta_{Q}\right)\right]
\end{aligned}- $p^{πO}$是observation的分布。
- $H_j^t$是表示是否接受信息$O_b^t$的两点分布。
- $\pi\left(H_{j}^{t} \mid O_{j}^{t}, O_{b}^{t}\right)$是判断$O_b^t$的策略。
- $Q\left(O_{j}^{t}, E_{j}^{t}, a_{j}^{t} ; \theta_{Q}\right)$ 是Critic网络的评判标准。
信息中心网络:
- 对于每个Agent($L_j$),如果判断使用$O_b^j$,则意味着$O_b^j$满足$L_j$。
- 定一个函数$A(O_1^t,O_2^t,…,O_M^t,O_b^t)$去评价从向量$(O_1^t,O_2^t,…,O_M^t)$选择$O_b^t$:
$A(O_1^t,O_2^t,...,O_M^t,O_b^t) = \sum_{j=1}^M H_j^t \cdot Q(O_{j}^{t}, E_{j}^{t}, a_{j}^{t} ; \theta_{Q})$ - 如果$H_j^t=1$,则将其计入标准中。
- 需要训练的参数为$\theta_{IC}$,Loss Function:
$\begin{array}{l}
\nabla_{\theta_{I C}} J\left(\theta_{I C}\right)=E_{s^{t} \sim \rho^{\pi}, O_{b} \sim \pi_{\theta_{I C}}}\left[\nabla_{\theta_{I C}} \log \pi\left(O_{b}^{t} \mid O_{1}^{t}, O_{2}^{t}, \ldots, O_{M}^{t}\right)\right.\\
\text { - } \left.A\left(O_{1}^{t}, O_{2}^{t}, \ldots, O_{M}^{t}, O_{b}^{t}\right)\right] \text {. }
\end{array}$- $\rho^π$代表全局状态$s^t$。
算法总览
