[文献阅读] Deep Reinforcement Learning for Task Offloading in Mobile Edge Computing Systems 移动边缘计算系统中任务卸载的深度强化学习

摘要与论文贡献

• CCF：A类
• 考虑了缘节点的未知负载水平动态，提出了一种基于drl的MEC系统分布式卸载算法。在该算法中，每个移动设备可以利用局部观察到的信息，包括其任务的大小、其队列的信息和边缘节点的历史负载水平，以分散的方式确定卸载决策。此外，该算法能够处理时变的系统环境，包括新任务的到来、每个任务的计算需求以及其他移动设备的卸载决策。

---

参数

参数	描述
m	移动设备
n	边缘计算节点
$k_m(t)$	t时隙到达m的任务,若无新任务到达$k_m(t)=0$
$\lambda_m(t)$	t时隙开始时队头任务的大小，若无新任务到达$k\lambda_m(t)=0$
$\rho_m$	$k_m(t)$需要的处理频率
$l_m^{comp}(t)$	在计算队列上$k_m(t)$被处理完成或被丢弃的时间
$\delta_m^{comp}(t)$	在计算队列上$k_m(t)$等待被处理完成或被丢弃的时间
$l_m^{tran}(t)$	在传输队列上$k_m(t)$被处理完成或被丢弃的时间
$\delta_m^{tran}(t)$	在传输队列上$k_m(t)$等待被处理完成或被丢弃的时间
$k_{m,n}^{edege}(t)$	在边缘设备n上对应的m队列中的任务
$\lambda_{m,n}^{edege}(t)$	$k_{m,n}^{edege}(t)$的任务大小
$f_n^{edege}$	边缘设备n的处理能力
$q_{m,n}^{edege}(t)$	t时隙n中设备m任务的队列长度
$B_n(t)$	n中的活动队列集
$e_{m,n}^{edge}(t)$	t时隙结束时被遗弃的任务数
$l_{m,n}^{edge}(t)$	$k_m(t)$将要被处理时的时隙
$\hat{l}_{m,n}^{edge}(t)$	$k_m(t)$开始被处理时的时隙

---

系统模型

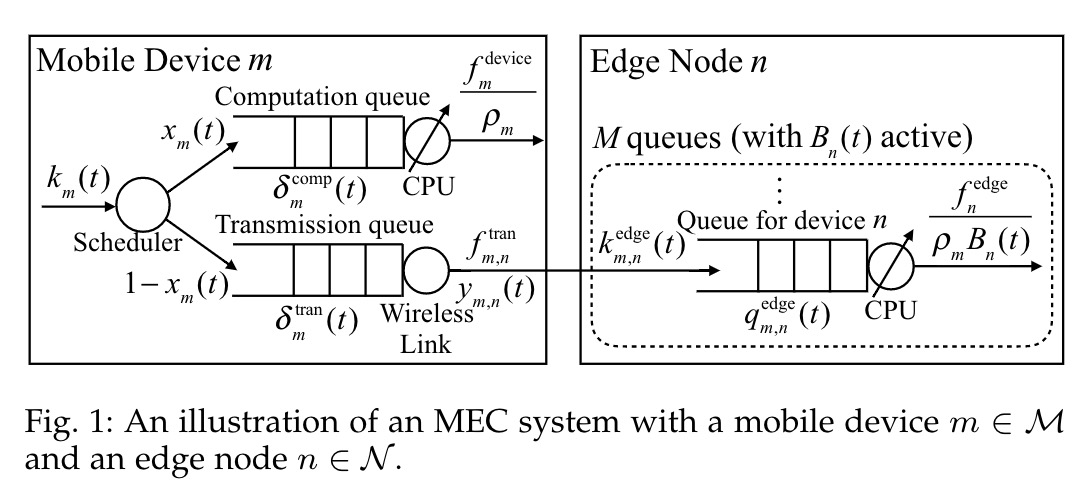
假设有一组时隙序列 $\mathcal{T}={1,2,…,T}$,每个时隙持续$\Delta$秒。

移动设备m模型

• 对于每个$\Delta$，我们假设移动设备要么有新任务到达，要么么有新任务到达， 且每个$\Delta$都很小(e.g. $\Delta = 0.1 $秒)。
• 任务可以被放到计算队列(在本地处理)或者传输队列(在边缘节点上处理)。
• 对于队列中的任务，我们假设任务处理(传输)在一个$\Delta$内完成，而下一个任务将在下一个$\Delta$开始。

任务模型

• $t \in \mathcal{T}$，当m有一个新的任务到达时，定义 $k_m(t)$ 为该任务的索引，如果没有任务到达,$k_m(t)=0$，$ \lambda_m(t)$表示在时隙t开始时队列开头新到达的bit数，如果在t开始时有一个新的任务$k_m$(t)到达，那么$\lambda_m(t)$的大小就是$k_m(t)$的大小，否则$\lambda_m(t)$=0。
• 将$k_m(t)$设为离散的，有$\Lambda \equiv {\lambda_1,\lambda_2,…,\lambda_{|\Lambda|}} , \lambda_m(t) \in \Lambda \cup {0}$。
• $k_m(t)$需要 $\rho_m$ 的处理频率。
• $k_m(t)$有一个截止时间$\mathcal{T}_m$,如果$k_m(t)$在$t+\mathcal{T}_m-1$结束时没有被处理完就被丢弃。

任务卸载设计

• 每当有一个新任务到达时，(a)在本地计算还是卸载。(b)卸载哪个边缘服务器上。 $x_m(t)$ 表示卸载地点。1：在本地计算，0:卸载到边缘服务器上。
• 在t开始时，$\lambda(t)x_m(t)$ 表示在移动设备本地计算队列的bits。$\lambda(t)(1-x_m(t))$ 是移动设备m到达传输队列的bits。
• 二元变量 $y_{m,n}(t) \in {0,1}$ 表示$k_m(t)$是否卸载，1:卸载，0:不卸载。为方便表示，引入向量$\textbf{y}_m = {y_{m,n}(t),n \in \mathcal{N}}$，假设每个任务只能被卸载到一个边缘服务器：

$$\sum _{n\in \mathcal{N}}{y}_{m,n}(t)=\mathbb{1}(x_m(t)=0),m\in \mathcal{M},t\in \mathcal{T}$$

其中指示器$\mathbb{1}(z \in \mathcal{Z}) = 1$ 如果$(z \in \mathcal{Z})$，否则等于0。

计算队列

$f_m^{device}$ 表示每个时隙内的处理能力，设备m最大可以处理队列中 $\frac{f_m^{device}}{\rho_m}$ bits的数据。

• 如果t开始时,$k_m(t)$在队列内， $l_m^{comp}(t) \in \mathcal{T}$ 表示$k_m(t)$被处理或者被丢弃的时隙。如果$k_m(t)$不放入计算队列或$k_m(t)=0$则$l_m^{comp}(t) \in \mathcal{T} = 0$。

• $\delta_m^{comp}(t)$ 表示$k_m(t)$放置在队列中等待处理的时隙数，移动设备将在决定放置哪个队列前计算$\delta_m^{comp}(t)$。给定$l_m^{comp}(t^{‘})， t^{‘} < t$，有

  $${\delta }_m^{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}(t)={[\underset{t^{\mathrm{\prime }}\in \{0,1,\dots ,t-1\}}{max}{l}_m^{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}\left(t^{\mathrm{\prime }}\right)-t+1]}^{+}$$

  其中$[z]^+ = \max \left \{ 0,z \right \} $，在t之前的所有任务要么都被处理，要么被丢弃。因此$\delta_m^{comp}(t)$确定任务$k_m(t)$应等待处理的时隙数。

• $k_m(1)$被放在计算队列中，它的处理在时隙5内完成，那么$l_m^{comp}(1) = 5$。
• 同时，$k_m(2)=0$，那么$l_m^{comp}(2) = 0$。
• 在时隙3开始时，如果$k_m(3)$被放入计算队列中，那么将在时隙$l_m^{comp}(1) = 5$后处理它，因此他必须等待$\delta_m^{comp}(3) = [max \left \{ 5,0 \right \} - 3 + 1]^+ = 3$个时隙。

• 如果m在t开始时处理$k_m(t)$，那么将在时隙$l_m^{comp}(t)$结束时完成处理或丢弃。$$\begin{array}{r}{l}_m^{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}(t)=min\{t+{\delta }_m^{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}(t)+\left[\frac{{\lambda }_m(t)}{f_m^{\text{device }}/{\rho }_m}\right]-1\\ t+{\tau }_m-1\}\end{array}$$

前半段为当前时隙+等待时隙+需要处理的时间-1，表示任务被处理。后半段表示任务被丢弃。$k_m(t)$将在$\delta_m^{comp}(t)$个时隙才开始处理。

传输队列

• $f_m^{tran}$ 表示每个时隙从m到n的传输容量。
• 在t开始时，$k_m(t)$被放在传输队列，同样$l_m^{tran}(t)$表示$k_m(t)$被传输或被丢弃的时隙。如果$k_m(t)$没有被放在传输队列中，$l_m^{tran}(t)=0$。
• 同样$${\delta }_m^{\mathrm{t}\mathrm{r}\mathrm{m}\mathrm{a}}(n)={[\underset{t^{\mathrm{\prime }}\in \{0,1,\dots ,t-1\}}{max}{l}_m^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}}\left(t^{\mathrm{\prime }}\right)-t+1]}^{+}$$

$$\begin{array}{r}{l}_m^{\mathrm{tran}}(t)=min\{t+{\delta }_m^{\mathrm{tran}}(t)+\left[\sum _{n\in \mathcal{N}}\frac{y_{m,n}(t){\lambda }_m(t)}{f_{m,n}^{\mathrm{tran}}}\right]-1\\ t+{\tau }_m-1\}\end{array}$$

前半段为当前时隙+等待时间+传输时间，后半段为丢弃时间。

在边缘节点上

• 每个n包含M个队列,每个队列对应一个传输设备。
• 在一个时隙中的边缘节点接收到卸载任务后，该任务将在下一时隙开始时被放在相应的队列中。
• 如果m的任务在t开始时被放在相应的队列中，记为 $k_{m,n}^{edege}(t)$。
• 如果任务$k_m(t^{‘})$在t-1时隙放到n中，那么$k_{m,n}^{edege}(t)=k_m(t^{‘})$。
• 如果t开始时，没有任务在队列中，则$k_{m,n}^{edege}(t)=0$，$\lambda_{m,n}^{edege}(t) \in \Lambda \cup {0}$表示大小。

边缘节点上的队列

$q_{m,n}^{edege}(t)$ 表示t时隙n中m设备任务的队列长度。

• 如果m队列被称为活动队列，则满足：
  • 在时隙t开始新任务到达，即$\lambda_{m,n}^{edege}(t) > 0$。
  • 在t-1时隙结束时队列不为0,$q_{m,n}^{edege}(t-1) > 0$，即队列中存在任务。
• $\mathcal{B}_n(t)$ 表示n中的活动队列集。
  • $\mathcal{B}_{n}(t)=\left\{m \mid m \in \mathcal{M}, \lambda_{m, n}^{\text {edge }}(t)>0 \text { or } q_{m, n}^{\text {edge }}(t-1)>0\right\}$.
  • $B_n(t)$ 表示活动队列数量，$B_n(t) = \mathcal{B}_n(t)$。
• 在时隙t内，n中的活动队列共享n的处理能力，因此n最大可以处理的任务数为：$\frac{f_n^{edege}}{\rho_nB_n(t)}$。
• 假设一个任务在一个时隙内处理完成，那么下一个任务将在下一个时隙才开始处理。
• 设 $e_{m,n}^{edge}(t)$ 为在t时隙被丢弃的任务数，则队列长度为：$$\begin{array}{rl}{q}_{m,n}^{\text{edge }}(t)=& [q_{m,n}^{\text{edge }}(t-1)+{\lambda }_{m,n}^{\text{edge }}(t)\\ & {-\frac{f_n^{\text{edge }}}{{\rho }_m{B}_n(t)}\mathbb{1}(m\in {\mathcal{B}}_n(t))-e_{m,n}^{\text{edge }}(t)]}^{+}.\end{array}$$

先前队列长度+新到达的任务数-应处理的数据-被丢弃的任务大小。

任务的处理或丢弃

• 同理,$l_{m,n}^{edge}(t)$表示任务处理或丢弃的时间，如果$k_{m,n}^{edge}(t) = 0$，那么$l_{m,n}^{edge}(t) = 0$。由于不确定将会被放在哪个边缘设备上，移动设备不知道$l_{m,n}^{edge}(t)$的值，知道关联任务$k_{m,n}^{edge}(t)$被处理，所以我们定义$\hat{l}_{m,n}^{edge}(t)$表示$k_{m,n}^{edge}(t)$开始处理的时隙。

  $${\hat{l}}_{m,n}^{\text{edge }}(t)=max\{t,\underset{t^{\mathrm{\prime }}\in \{0,1,\dots ,t-1\}}{max}{l}_{m,n}^{\text{edge }}\left(t^{\mathrm{\prime }}\right)+1\},$$

• 约束：

$$\begin{array}{l}\sum _{t^{\mathrm{\prime }}={\hat{l}}_{m,n}^{\text{edge }}(t)}^{l_{m,n}^{\text{edge }}(t)}\frac{f_n^{\text{edge }}}{{\rho }_m{B}_n\left(t^{\mathrm{\prime }}\right)}\mathbb{1}(m\in {\mathcal{B}}_n\left(t^{\mathrm{\prime }}\right))\ge {\lambda }_{m,n}^{\text{edge }}(t)\\ \sum _{t^{\mathrm{\prime }}={\hat{l}}_{m,n}^{\text{edge }}(t)}^{l_{m,n}^{\text{edge }}(t)-1}\frac{f_n^{\text{edge }}}{{\rho }_m{B}_n\left(t^{\mathrm{\prime }}\right)}\mathbb{1}(m\in {\mathcal{B}}_n\left(t^{\mathrm{\prime }}\right))<{\lambda }_{m,n}^{\text{edge }}(t).\end{array}$$

第一个约束代表从$\hat{l}_{m,n}^{edge}(t)$到$l_{m,n}^{edge}(t)$的处理能力不小于${k}_{m,n}^{edge}(t)$的大小。第二个约束代表从$\hat{l}_{m,n}^{edge}(t)$到$l_{m,n}^{edge}(t)-1$的处理能力不大于${k}_{m,n}^{edge}(t)$的大小。个人推测：得有足够的能力开始处理${k}_{m,n}^{edge}(t)$？

---

MEC上的任务卸载问题

State

• 对于移动设备m，有 $s_m(t) = (\lambda_m(t), \delta_m^{comp}(t),\delta_m^{tran}(t),q_m^{edge}(t-1),H(t))$ 。
  • 向量$q_m^{edge}(t-1) = (q_{m,n}^{edge}(t-1),n \in \mathcal{N})$。
  • 矩阵$H(t)$包含了前一个T步骤(从时隙$t-T^{step}$到时隙$t-1$)时隙中每个n的负载水平。(活动队列的数量)。$H(t)$的大小为为$T^{step} \cdot N$，${H(t)}_{i,j}$表示矩阵i,j的值。对应从时隙 $t-T^{step}$ 开始的第i个时隙总边缘节点j的活动队列数量 。例如在时隙$t-T^{step}+i-1$中，${H(t)}_{i,j} = B_j(t-T^{step}+i-1)$。
• $\mathcal{S}$ 为状态空间，则$\mathcal{S} = \Lambda \cdot \{0,1,…,T\}^2 \cdot \mathcal{Q}^N \cdot \{0,1,…,M\}^{T^{step} \cdot N}$。
• 设备m在时隙开始时获得$\lambda_m(t), \delta_m^{comp}(t),\delta_m^{tran}(t)$。

Action

当$k_m(t)$到达时：(a)是否卸载，（b)卸载到哪里。

• 动作由一个向量表示: $a_m(t)=(x_m(t),y_m(t))$

Cost

• 用 $d_m(x_m(t),a_m(t))$ 来表示任务$k_m(t)$的延迟,给定观察状态$s_m(t)$和动作$a_m(t)$，有$d_m(x_m(t),a_m(t)) = l_m^{comp}(t) - t + 1$。
• 如果$x_m(t)=0$，即卸载到边缘节点，有：$$\begin{array}{rl}{d}_m& ({\mathit{s}}_m(t),{\mathit{a}}_m(t))\\ =& \sum _{n\in \mathcal{N}}\sum _{t^{\mathrm{\prime }}=t}^T\mathbb{1}(k_{m,n}^{\text{edge }}\left(t^{\mathrm{\prime }}\right)=k_m(t))l_{m,n}^{\text{edge }}\left(t^{\mathrm{\prime }}\right)-t+1\end{array}$$

具体的说$k_m(t)$的延迟就是等待处理或丢弃的时隙数。

• Cost:$C_m(x_m(t),a_m(t)) = d_m(x_m(t),a_m(t))$,如果被任务被丢弃，则$C_m(x_m(t),a_m(t))= C$,C为一个惩罚常数，C>0。如果$k_m(t) = 0$，那么$C_m(x_m(t),a_m(t))= 0$。

后使用$C_m(t)$简化表达。

问题表述

• $π_m:\mathcal{S} \to \mathcal{A}$。
• 目标：找到一个最优策略$π_m^{\ast}$，使得cost最小。$${\pi }_m^{\ast }=\arg {\mathrm{minimize}}_{{\pi }_m}\mathbb{E}[\sum _{t\in \mathcal{T}}{\gamma }^{t-1}{c}_m(t)\mid {\pi }_m]$$

---

基于DRL的卸载算法

使用q值。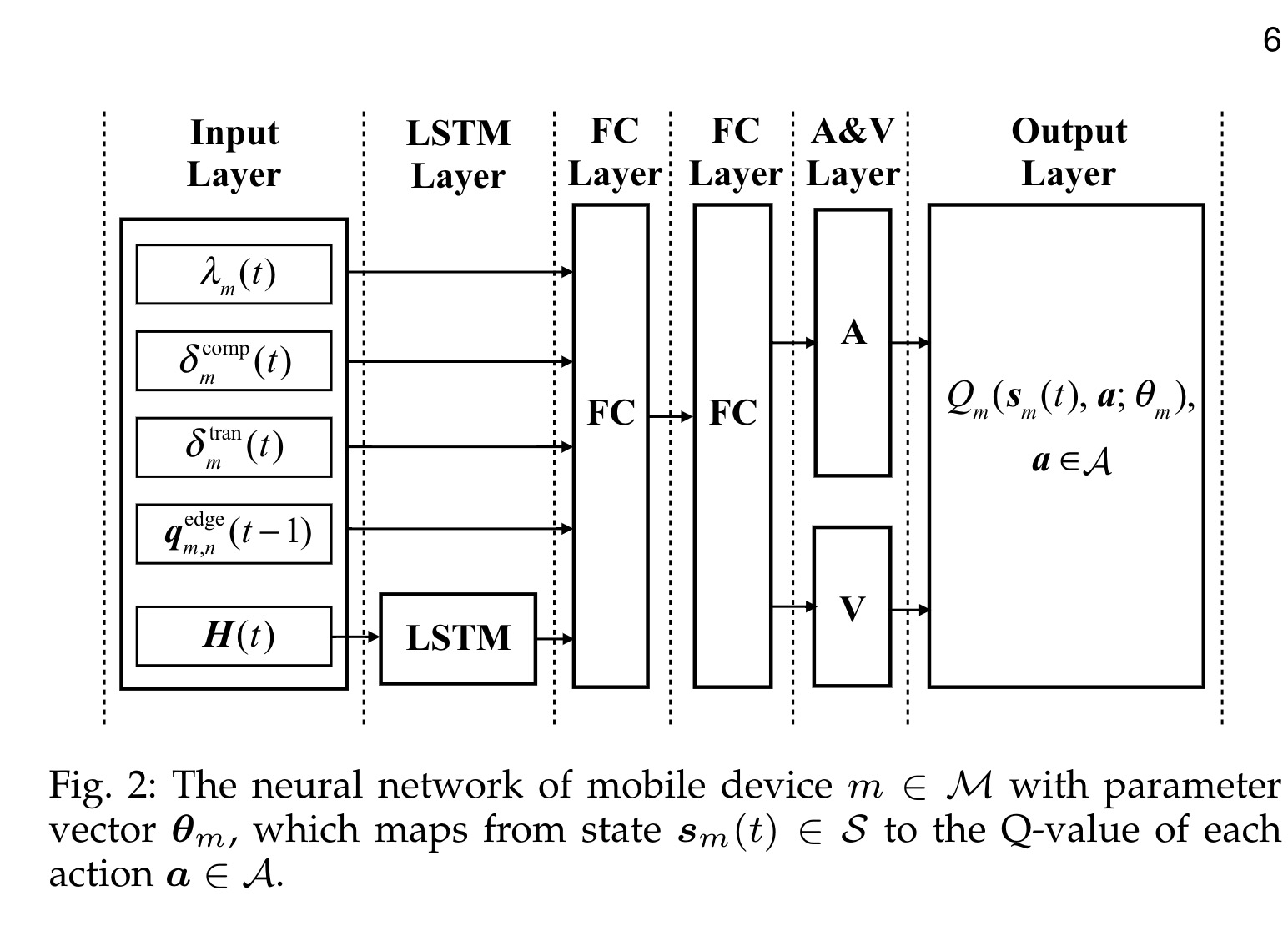

神经网络结构

如图所示，由一个输入层，一个LSTM层，两个全连接层一个优势和价值层(A&V)以及一个输出层组成。

输入层

输入层输入一组向量$(\lambda_m(t),\delta_m^{comp}(t),\delta_m^{tran},q_{m,n}^{edge}(t-1),H(t))$ , 其中$H(t)$被送入LSTM层，其他直接进入到全连接层。

LSTM层

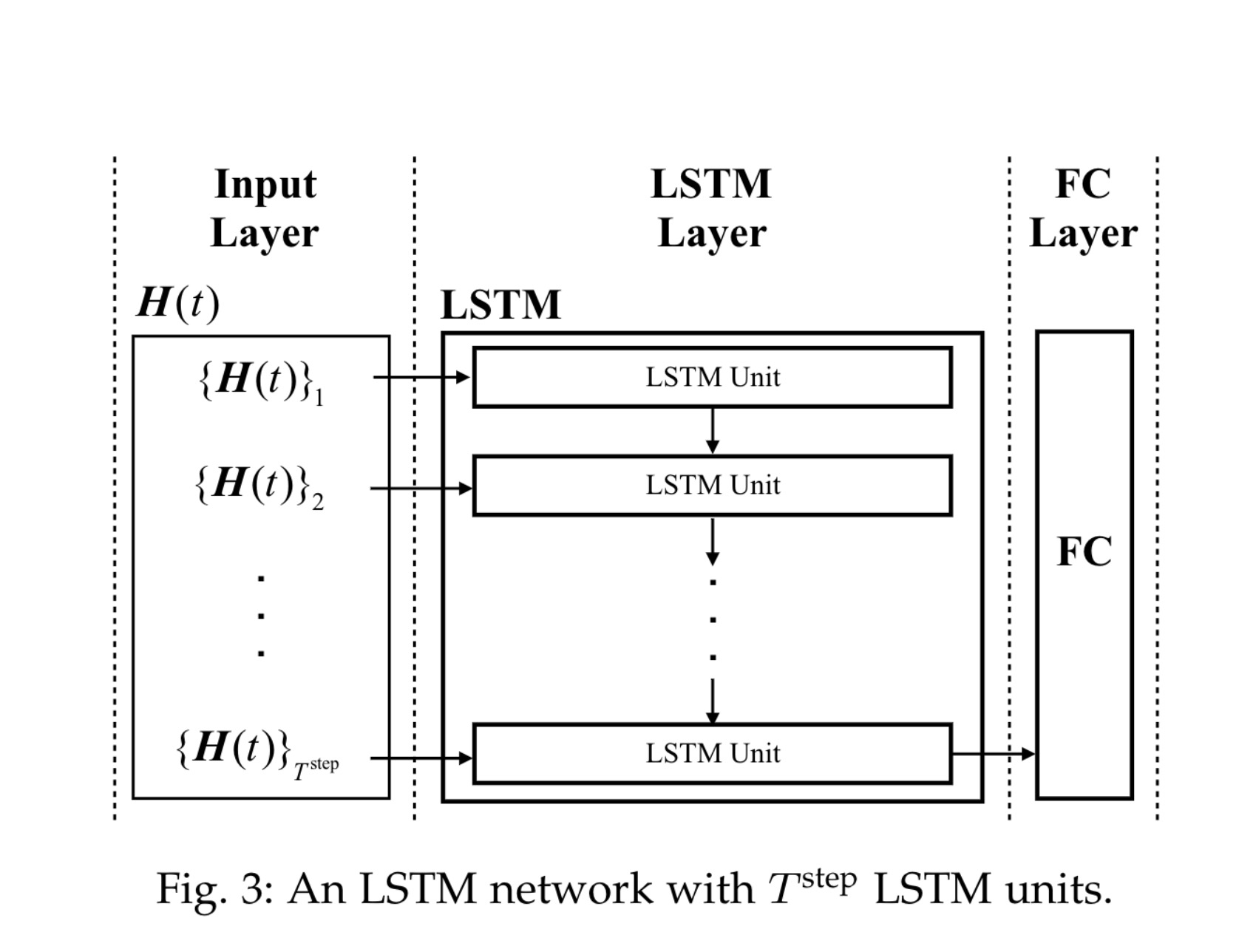
该层负责学习边缘节点上的动态负载水平，使用历史记录来估计未来的负载水平，结构如图3所示。每个LSTM unit都以一行$\{H(t)\}_i$作为输入，这些LSTM unit按顺序连接，以跟踪他们的序列变化，可以得到边缘节点负载水平的变化。LSTM网络将输出最后一个LSTM unit到下一层的神经元。

全连接层

使用ReLU函数作为激活函数。

A&V层和输出层

这一层采用Double-DQN的技术，使用$A_m(s_m(t),a;\theta_m)$表动作优势函数,$V_m(s_m(t);\theta_m))$为状态价值函数。$\theta_m$在DRL的过程中更新。其Q值表示为：

$$\begin{array}{rl}{Q}_m({\mathit{s}}_m(t),\mathit{a};{\mathit{\theta }}_m)& =V_m({\mathit{s}}_m(t);{\mathit{\theta }}_m)+(A_m({\mathit{s}}_m(t),\mathit{a};{\mathit{\theta }}_m)\\ & -\frac{1}{|\mathcal{A}|}\sum _{{\mathit{a}}^{\mathrm{\prime }}\in \mathcal{A}}{A}_m({\mathit{s}}_m(t),{\mathit{a}}^{\mathrm{\prime }};{\mathit{\theta }}_m))\end{array}$$

Q值：当前状态价值+（当前动作价值-平均动作价值）

基于DRL的算法

• 算法部分分为在移动设备上的算法和在边缘设备上的算法。
• $n_m \in \mathcal{N}$ 表帮助移动设备m训练的边缘节点n。这个边缘节点n可以是移动设备m具有最大传输容量的边缘节点。用 $\mathcal{M}_n \subset \mathcal{M}$ 表示由边缘节点n训练的移动设备集。
• 在这个算法中，边缘节点n包含了replay memory($D_m$)用于存储在时隙t内移动设备m的多条Transition$(s_m(t),a_m(t),c_m(t),s_m(t+1))$以及两个神经网络： Eval_net 和 Target_Net 以及对应的Q值 $Q_m^{Eval}(s_m(t),a;\theta_m^{Eval})$ 和 $Q_m^{Target}(s_m(t),a;\theta_m^{Target})$ 。其中两个Q值只有$\theta$值不同。

在移动设备m上的算法

如图所示，在m上：

• 初始化$s_m(1)$,例如:$s_m(1) = (\lambda_m(1), \delta_m^{comp}(1),\delta_m^{tran}(1),q_m^{edge}(0),H(1))$

其中$q_{m,n}^{edge}(0)=0$对于所有$n \in \mathcal{N}$,$H(1)$是一个数值全为0的矩阵。

• 当有$k_m(t)$到达时，发送一个请求参数 (parame-terrequest) 给边缘节点$n_m$。
• 收到边缘节点$n_m$的Eval_Net返回的参数$\theta_m^{Eval}$。
• 设备m选择$k_m(t)$接下来的action:$${\mathit{a}}_m(t)=\{\begin{array}{c}\text{select a random action from }\mathcal{A},\text{ with prob. }ϵ\text{, }\\ \arg \underset{\mathit{a}\in \mathcal{A}}{min}{Q}_m^{\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{l}}({\mathit{s}}_m(t),\mathit{a};{\mathit{\theta }}_m^{\text{Eval }}),withprob.1-ϵ,\end{array}$$

其中$\epsilon$是一个概率常数，为greedy(epsilon)。

• 由于任务的处理和传输可能持续多个时隙，所以在时隙t+1可能观察不到任务$k_m(t)$的延迟(成本)$c_m(t)$。相对的，可以观察一组任务$k_m(t)^{‘}$的成本，$t^{‘} ≤ t$。我们定义$\tilde{\mathcal{T}}_{m,t} \subset \mathcal{T} $为一组时隙，使得每个$k_m(t^{‘})$都在时隙中被处理。$\tilde{\mathcal{T}}_{m,t}$定义如下：$$\begin{array}{c}{\tilde{\mathcal{T}}}_{m,t}=\{t^{\mathrm{\prime }}\mid t^{\mathrm{\prime }}=1,2,\dots ,t,{\lambda }_m\left(t^{\mathrm{\prime }}\right)>0,x_m\left(t^{\mathrm{\prime }}\right)l_m^{\text{comp }}\left(t^{\mathrm{\prime }}\right)\\ +(1-x_m\left(t^{\mathrm{\prime }}\right))\sum _{n\in \mathcal{N}}\sum _{i=t^{\mathrm{\prime }}}^t\mathbb{1}(k_{m,n}^{\text{edge }}(i)=k_m\left(t^{\mathrm{\prime }}\right))l_{m,n}^{\text{edge }}(i)=t\}\end{array}$$

具体的说，如果任务$k_m(t^{‘})$已经在时隙t中被处理，则$t^{‘}$被集合$\tilde{\mathcal{T}}_{m,t}$包含。因此在时隙t+1的开始，移动设备可观察到一组成本$\{c_m(t^{‘}) , t^{‘} \in \tilde{\mathcal{T}}_{m,t}\}$，其中$\tilde{\mathcal{T}}_{m,t}$可以是某些m和t的空集。然后对于每个$k_m(t^{‘})$，设备m发送他们的transition$(s_m(t^{‘}),a_m(t^{‘}),c_m(t^{‘}),s_m(t^{‘}+1))$到边缘节点$n_m$上。

在边缘节点n上的算法

• 初始化$D_m$，Eval_net 和 Target_Net 。

• 等待m发送信息：

  • 如果接收的是一个请求参数 (parameterrequest) 则发送当前 Eval_net 的参数$\theta_m^{Eval}$给m。

  • 如果接收到的是一条transition$(s_m(t),a_m(t),c_m(t),s_m(t+1))$：

    • 将他放入到$D_m$中，如果$D_m$已满，则采用FIFO方法管理。

    • 边缘节点将会用这些transition来训练神经网络（大概10-20步，详见算法），用于更新Eval_net 的参数$\theta_m^{Eval}$。（使用Double-DQN方法）

      • 计算TD Target：从中随机抽样$\mathcal{I}$条transition来计算$\hat{Q}_m^{Target}$:
        $\hat{Q}_{m, i}^{\text {Target }}=c_{m}(i)+\gamma Q_{m}^{\text {Target }}\left(\boldsymbol{s}_{m}(i+1), \boldsymbol{a}_{i}^{\text {Next }} ; \boldsymbol{\theta}_{m}^{\text {Target }}\right)$
        其中$a_i^{Next}$由Eval_Net的状态$s_m(t+1)$下的最小Q值动作给出：

        $${\mathit{a}}_i^{\mathrm{N}\mathrm{e}\mathrm{x}\mathrm{t}}=\arg \underset{\mathit{a}\in \mathcal{A}}{min}{Q}_m^{\text{Eval }}({\mathit{s}}_m(i+1),\mathit{a};{\mathit{\theta }}_m^{\text{Eval }})$$

      • 计算TD error：使用最小化损失函数计算：

        $$\begin{array}{r}L({\mathit{\theta }}_m^{\text{Eval }},{\hat{\mathit{Q}}}_m^{\text{Target }})=\frac{1}{|\mathcal{I}|}\sum _{i\in \mathcal{I}}(Q_m^{\text{Eval }}({\mathit{s}}_m(i),{\mathit{a}}_m(i);{\mathit{\theta }}_m^{\text{Eval }})\\ {-{\hat{Q}}_{m,i}^{\text{Target }})}^2\end{array}$$

      • 每过一定步骤，更新网络参数：$\theta_m^{Target} = \theta_m^{Eval}$。

---

论文地址

Tang, Ming, and Vincent WS Wong. “Deep reinforcement learning for task offloading in mobile edge computing systems.” IEEE Transactions on Mobile Computing (2020).