[强化学习]连续控制

确定策略梯度 Deterministic Policy Gradient, DPG

• 使用一个确定策略网络(actor): $a=π(s;θ)$.
• 使用一个价值网络(critic): $q(s,a;w)$.
• critic输出一个数值用来评价动作a的好坏。
  
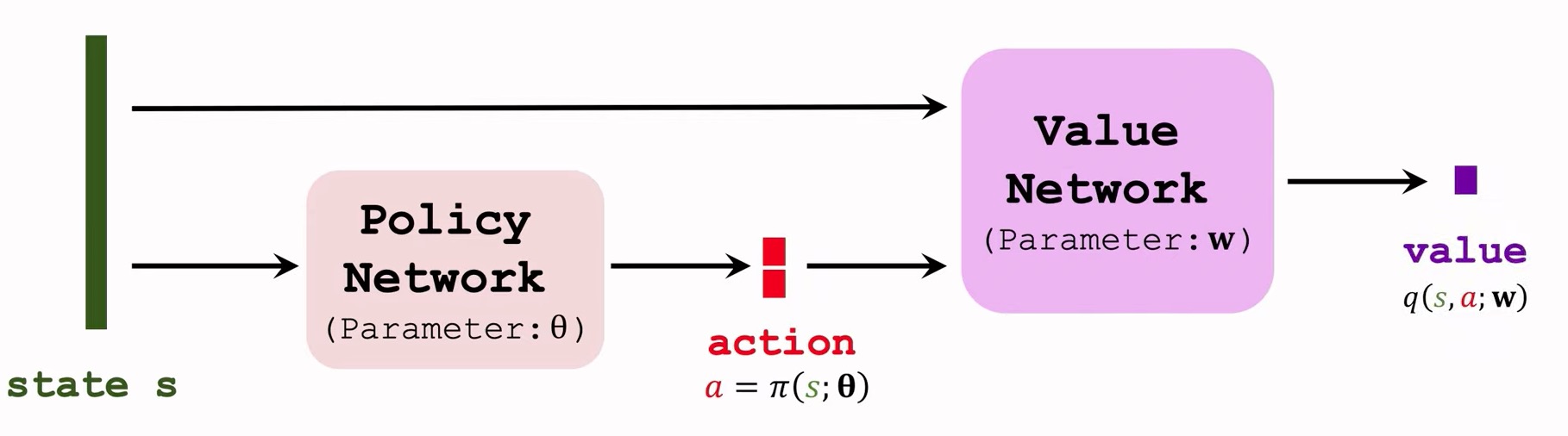
  确定策略梯度 (DPG) 方法的示意图。策略网络π(s;θ)的输入是状态s,输出是动作a(d维向量)。价值网络q(s,a;w)的输入是状态s和动作a,输出是价值(实数)。我们需要更新这两个网络。

使用TD算法更新价值网络

详见TD算法章节。可以使用Double DQN来改进网络。

使用DPG更新策略网络

训练策略网络需要价值网络的帮忙。

• 价值网络 $q(s,a,;w)$评价动作a的好坏。
• 改进θ让评价网络认为$a=π(s;θ)$更好。
• 更新θ来让$q(s,a;w) = q(s,π(s;θ);w)$增大。

• 目标：让$q(s,a;w)$更大，对于$a=π(s;θ)$.
  状态s是固定的，价值网络也是固定的，那么唯一会影响价值q的因素就是策略网络的θ。所以我们计算q关于θ的梯度，做梯度上升更新θ，让q更大，这个梯度叫做DPG。
• DPG:$$\mathbf{g}=\frac{\mathrm{\partial }q(s,\pi (s;\mathit{\theta });\mathbf{w})}{\mathrm{\partial }\mathit{\theta }}=\frac{\mathrm{\partial }a}{\mathrm{\partial }\mathit{\theta }}\cdot \frac{\mathrm{\partial }q(s,a;\mathbf{w})}{\mathrm{\partial }a}$$

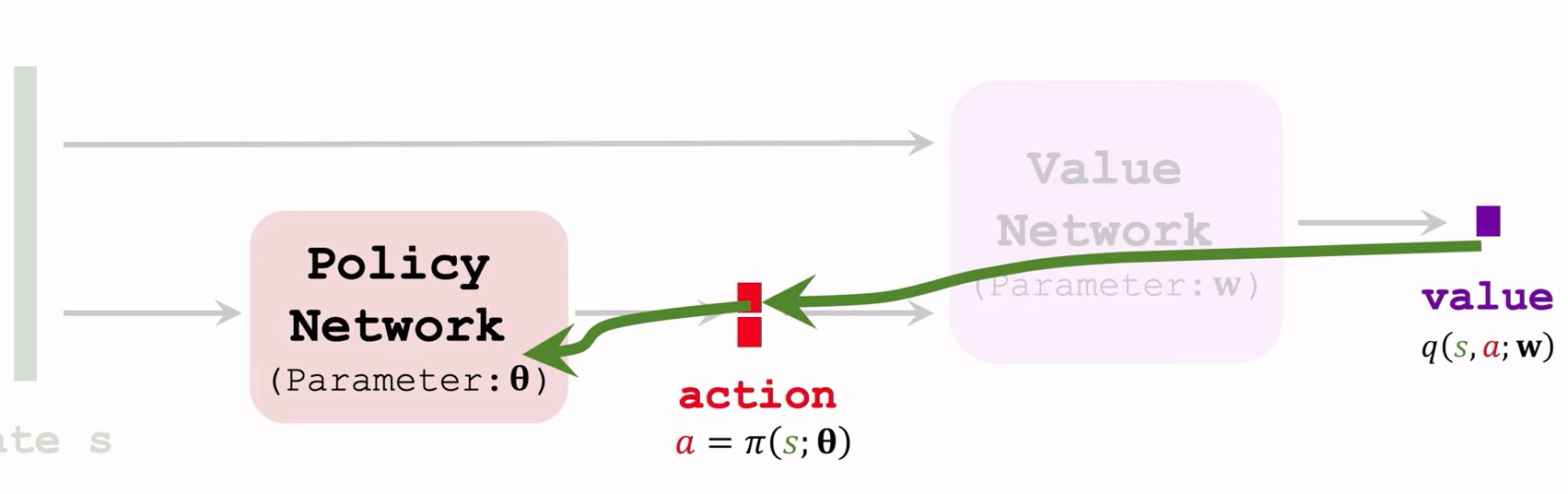
使用反向传播来更新梯度。

• 梯度上升:$\theta \gets \theta + \beta \cdot g$. $\beta$为学习率。

随机策略

基本思路

先考虑动作自由度等于1，也就是所动作a是实数，动作空间$\mathcal{A} \subset \mathbb{R}$。把动作的均值记作µ(s)，标准差记作σ(s)，它们都是状态s的函数。用正态分布的概率 密度函数作为策略函数：

$$\pi (a\mid s)=\frac{1}{\sqrt{6.28}\cdot \sigma (s)}\cdot \exp (-\frac{[a-\mu (s){]}^2}{2\cdot {\sigma }^2(s)})$$

等式的右边为正态分布的概率密度函数：$\mathcal{N}(µ,σ^2)$。
我们可以这样做控制:
1.观测到当前状态s，预测均值$\hat{µ}=µ(s)$和标准差$\hat{σ}=σ(s)$。
2.从正态分布中做随机抽样$a ∼ \mathcal{N}(\hat{µ},\hat{σ^2})$;智能体执行动作a。
然而我们并不知道$µ(s)$和$σ(s)$是怎么样的函数。一个很一个很自然的想法是用神经网络来近似这两个函数。把神经网络记作$µ(s;θ)$和$σ(s;θ)$，其中θ表示神经网络中的可训练参数。但实践中最好不要直接近似标准差σ，而是近似方差对数${lnσ^2}^2$。定义两个神经网络：$µ(s;θ)$和$ρ(s;θ)$
分别用于预测均值和方差对数。可以按照下图来搭建神经网络。神经网络的输入是状态s,输出为$µ(s;θ)$和$ρ(s;θ)$。

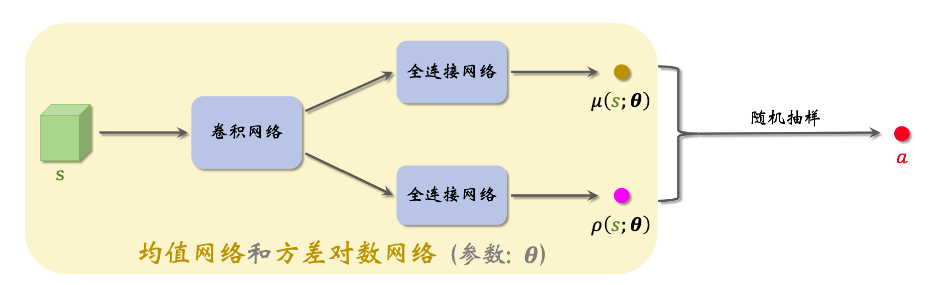
1.观测到当前状态s，计算均值$\hat{µ}=µ(s)$，方差对数$\hat{ρ}=ρ(s)$，以及方差$\hat{σ}^2 = exp(\hat{ρ})$。
2.从正态分布中做随机抽样$a ∼ \mathcal{N}(\hat{µ},\hat{σ^2})$;智能体执行动作a。

实际做控制的时候，我们只需要神经网络$µ(s;θ)$和$ρ(s;θ)$用不到真正的策略网络$π(a|s;θ)$。

随机高斯策略网络

上面假设的问题自由度d=1,但在实际中d往往大于1，那么此时的动作a是d维向量。此时我们需要让两个输出$µ(s;θ)$和$ρ(s;θ)$都为d维向量。
用标量$a_i$表示动作向量$a$的第$i$个元素。用函数$µ_i(s;θ)$和$ρ_i(s;θ)$分别表示$µ(s;θ)$和$ρ(s;θ)$的第$i$个元素。那么有$a_i ∼ \mathcal{N}(\hat{µ_i},\hat{σ_i^2})$,

训练策略网络

• 构造一个辅助神经网络帮助计算策略梯度。
• 用策略梯度方法训练策略网络:
  • REINFORCE
  • Actor-Critic

构造辅助神经网络

策略梯度为：

$$\pi (\mathbf{a}\mid s;{\mathit{\theta }}^{\mu },{\mathit{\theta }}^{\rho })=\prod _{i=1}^d\frac{1}{\sqrt{6.28}{\sigma }_i}\cdot \exp (-\frac{{(a_i-{\mu }_i)}^2}{2{\sigma }_i^2})$$

做控制的时候只需要均值网络$µ(s;θ)$和方差对数网络$ρ(s;θ)$不需要策略网络$π(a|s;θ)$。做训练的时候也不需要$π(a|s;θ)$,而是要用辅助网络$f(s,a;θ)$。总而言之，实际算法中不会出现π。

辅助神经网络具体是这样定义的：

$$f(s,\mathbf{a};\mathit{\theta })=\sum _{i=1}^d[-\frac{{\rho }_i}{2}-\frac{{(a_i-{\mu }_i)}^2}{2\cdot \exp \left({\rho }_i\right)}]$$

并且有:

$f(s,a;θ) = lnπ(a|s'θ) + const$

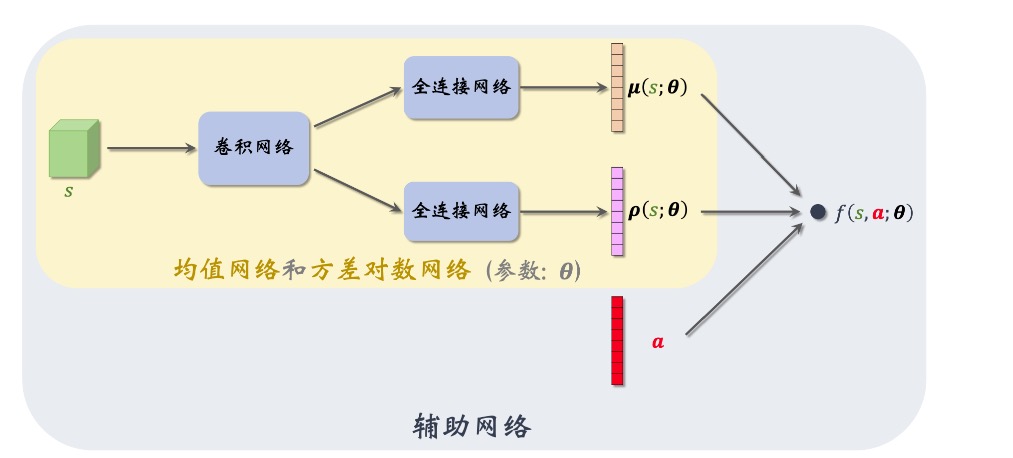
总而言之：使用$µ(s;θ^µ)$和$ρ(s;θ^ρ)$，构建出了$f(s,a;θ)$。其中θ包含了$θ^µ$和$θ^ρ$，训练时我们求$\frac{\partial f}{\partial θ}$，作为策略梯度。

训练策略梯度

随机策略梯度:$g(a) = \frac{\partial \ln \pi(a \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\left(Q_{\pi}(s, a)\right)$.

将$f(s,a;θ) = lnπ(a|s’θ) + const$代入，就可以得到：
$g(a) = \frac{\partial f(s,a;\theta)}{\partial \boldsymbol{\theta}}\left(Q_{\pi}(s, a)\right)$.

然后使用策略学习章节中的知识做梯度上升。

PPO