[强化学习]策略学习

发表于 2022-04-23 更新于 2022-05-10 收录于学习笔记

强化学习中的策略学习。包括REINFORCE with Baseline 以及A2C。

定义

使用一个策略网络$π(a|s;\theta)$来控制Agent。策略函数π的输入是状态s和动作a，θ 表示神经网络的参数，输出是一个0到1之间的概率值。
每当观测到一个状态s，就用策略函数计算出每个动作的概率值，然后做随机抽样，得到一个动作a，让智能体执行a。
一开始随机初始化θ，随后利用收集的状态、动作、奖励去更新θ。

状态价值函数: $\begin{aligned} V_{π} (s) & = E_{A \sim π} [Q_{π} (s, A)] \\ = \sum_{a} π (a ∣ s; θ) \cdot Q_{π} (s, a) \end{aligned}$

Policy Gradient

策略梯度函数就是$V_π$对θ的求导： $\begin{aligned} \nabla V_{π} (s) & = \sum_{a} \nabla π (a ∣ s; θ) \cdot (Q π ∣ s, a) \\ = \sum_{α} \nabla \frac{π (a ∣ s; θ)}{π (a ∣ s; θ)} \cdot π (a ∣ s; θ) \cdot Q_{π} (b, a) \\ = E_{A \sim π} [\nabla \ln π (A ∣ s; θ) \cdot Q π (s, a)] \end{aligned}$

其中$\nabla f(x) = f(x)\nabla logf(x)$

即：

\frac{\partial V_{π} (s)}{\partial θ} = E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ} \cdot Q_{π} (s, a)]

又有
$\begin{aligned}
E_{A \sim \pi}[\nabla \ln \pi(A \mid s ; \theta )\cdot Q \pi(s, a)]\approx \frac{1}{N} \sum_{n=1}^{N} \nabla \ln _{\pi}(A \mid s ; \theta) Q \pi\left(s, a\right) \\
=\frac{1}{N} \sum_{n=1}^{N} \sum_{n=1}^ \nabla \ln \pi\left(q_{t}^{n} \mid s_{t}^{n} ; \theta\right) Q \pi\left(s_t, a_t\right)\\
\end{aligned}$

看后面$ \sum_{n=1}^ \nabla \ln \pi\left(q_{t}^{n} \mid s_{t}^{n} ; \theta\right) Q \pi\left(s^{n}, a^{n}\right)$ ,我们可以理解为对于一个序列，求出每一次action在该state下的对数条件改了分布梯度并求和，然后乘以一个权重，这个权重就是该序列的奖励（Q值）。

简单的说就是如果最终奖励是正的，那么就增加这个序列出现的概率；反之如果是负的，就减少它出现的概率。

Baseline

我们为什么需要一个Baseline

我们知道，因为序列的可能性无穷多，所以我们会多次采样来估计这个概率分布，然后根据Reward的大小来调整买个序列出现的概率。

但这样就会导致：有一部分序列一直没被采样到，然而其他序列的Reward又一直是正的，导致其他序列的出现概率在疯狂增加，相应地这个序列出现的概率就会被挤占，最终导致明明这个序列的 Reward 很高，但是因为采样的问题被忽略掉了。

举个例子：如果一个人说“追女生被拒了我就血亏，而且反正我觉得我也追不到女生。相比而言，如果干脆就不追，我还能打游戏——不谈小赚，至少肯定不亏，我还很开心，是吧。”那么他可能就永远不会去追女生，但是他忽略掉了如果他追到女生的奖励会是非常大的，这也就是Policy Gradient的问题。

为了解决这个问题，所以我们添加一个 Baseline ，让一部分reward变成负的，在遇到负reward的时候，他就会减小这个序列出现的概率，这样就会把机会“让”给别的序列了。

从数学上来说就是减去一个值b，让奖励更均衡。

Baseline是一个函数 b,他可以是任何函数，但他不能依赖动作 A。

\begin{aligned} E_{A \sim π} [b \cdot \frac{\partial \ln π (A ∣ s; θ)}{\partial θ}] & = b \cdot E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ}] \\ = b \cdot \sum_{a} π (a ∣ s; θ) \cdot [\frac{1}{π (a ∣ s; θ)} \cdot \frac{\partial π (a ∣ s; θ)}{\partial θ}] \\ = b \cdot \sum_{a} \frac{\partial π (a ∣ s; θ)}{\partial θ} \\ = b \cdot \frac{\partial \sum_{a} π (a ∣ s; θ)}{\partial θ} \\ = b \cdot \frac{\partial 1}{\partial θ} = 0 . \end{aligned}

策略梯度又有：

\begin{array}{l} \frac{\partial V_{π} (s)}{\partial θ} \\ = E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ} \cdot Q_{π} (s, A)] - E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ} \cdot b] \\ = E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ} (Q_{π} (s, A) - b)] \end{array}

定义一：如果b与动作$A_t$无关，那么策略梯度就有：

\frac{\partial V_{π} (s)}{\partial θ} = E_{A \sim π} [\frac{\partial \ln π (A ∣ s; θ)}{\partial θ} (Q_{π} (s, A) - b)]

蒙特卡洛近似

我们设$g(A_t) = \left[\frac{\partial \ln \pi(A \mid s ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\left(Q_{\pi}(s, A)-b\right)\right]$，他依赖于随机变量$A_t$。我们对策略π做随机抽样，得到一个$a_t \sim π(·|s_t;θ)$并且计算$g(a_t)$。那么$g(a_t)$就是$g(A_t)$的 蒙特卡洛近似。训练策略网络的时候都是用$g(a_t)$。

训练的时候使用随机梯度上升来训练：
$θ \gets θ + \beta · g(a_t)$
b虽然不影响策略梯度函数$\mathbb{E}_{A \sim \pi}[g(A_t)]$,但他影响$g(a_t)$。
一个好的b可以让方差更小并让算法收敛得更快。

choice 1:b = 0。即不使用Baseline。

choice 2:b 是状态价值函数$V_π$。

REINFORCE with Baseline

折扣回报： $U_t$ = $R_t + \gamma · R_{t+1} + \gamma ^ 2 · R_{t+2} + … \gamma ^{n - t} · R_n$
动作价值函数: $Q_π(s_t, a_t) = \mathbb{E}[U_t|s_t,a_t]$
状态价值函数: $V_π(s_T) = \mathbb{E}[Q_π(s_T,A)|s_t ]$
这里使用状态价值函数当作Baseline，即$b = V_π(s_t)$。那么就有了随机策略梯度:$g(a_t) = \left[\frac{\partial \ln \pi(a_t \mid s_t ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\left(Q_{\pi}(s_t, A_t)- V_π(s_t)\right)\right]$.这个式子用$Q_π$和$V_π$两个未知数，我们需要对这两个未知数做蒙特卡洛近似：
- 蒙特卡洛近似：$Q_π(s_t,a_t) \approx u_t$: (REINFORCE)
  - 观察一条轨迹:$s_t,a_t,r_t,s_{t+1},a_{t+1},r_{t+1},…,s_n,a_n,r_n.$
  - t时刻开始所有的奖励做加权求和，得到retuen: $u_t = \sum_{i=1}^n \gamma^{i-t} · r_i$.
  - $u_t$是一个关于$Q_π(s_t,a_t)$无偏估计。
- $V_π$用神经网络做近似，得到$v(s;w)$，称为价值网络。
最后可以得到： $\frac{\partial V_{π} (s_{t})}{\partial θ} \approx g (a_{t}) \approx \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ} \cdot (u_{t} - v (s_{t}; w))$

一共做了三次近似：

使用一个样本 $a_t$ 来近似期望。(蒙特卡洛近似)

使用 $u_t$ 来近似 $Q_π(s_t,a_t)$ 。(蒙特卡洛近似)

使用价值网络 $v(s;w)$ 来近似 $V_t(s)$ 。

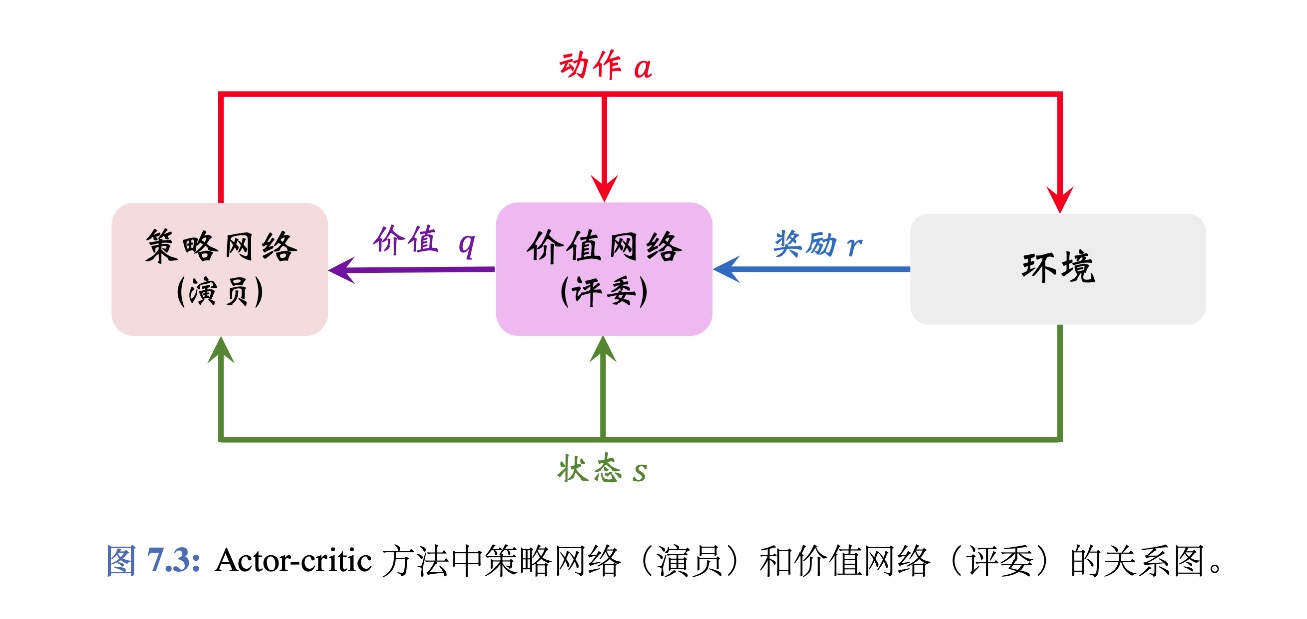
Policy and Value Network

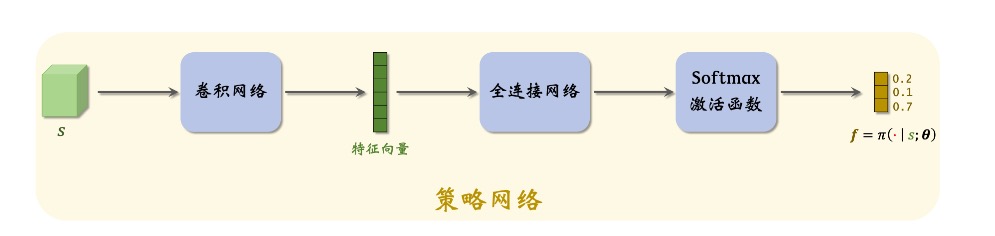
我们需要两个网络：一个策略网络和一个价值网络。策略网络用来控制Agent，价值网络起辅助作用，作为Baseline，帮助训练策略网络。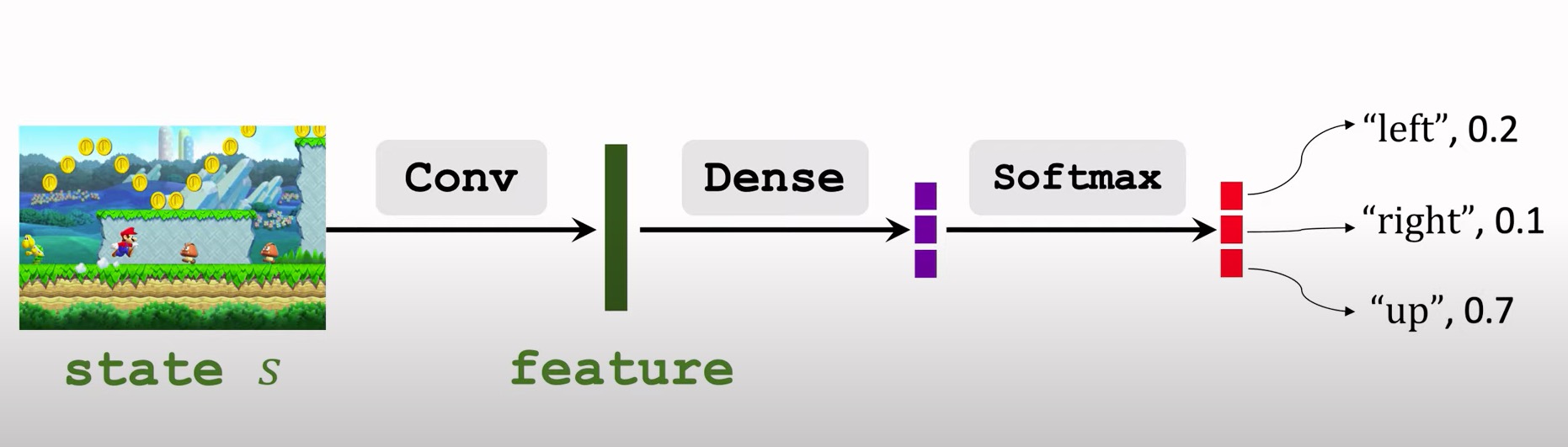

策略网络 π(a|s;θ) 的神经网络结构。输入是状态s，输出是动作空间中每个动作的概率值。举个例子，动作空间是A = {左,右,上}，策略网络的输出是三个概率值：π(左|s;θ) = 0.2，π(右|s;θ) = 0.1，π(上|s;θ) = 0.7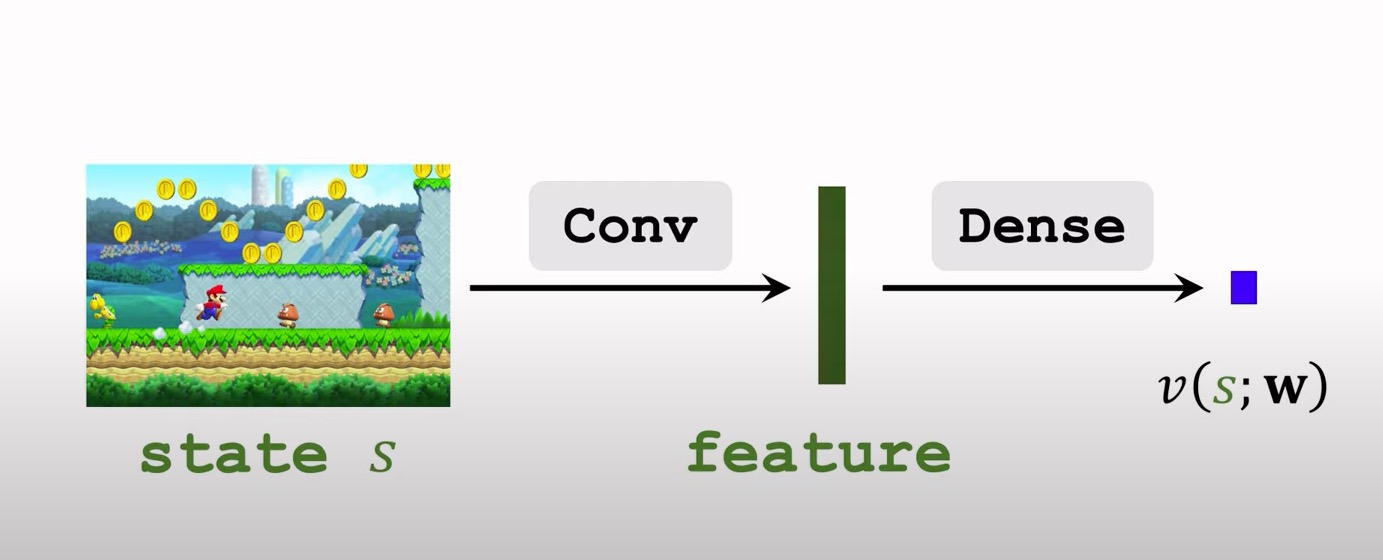

价值网络被用作Baseline。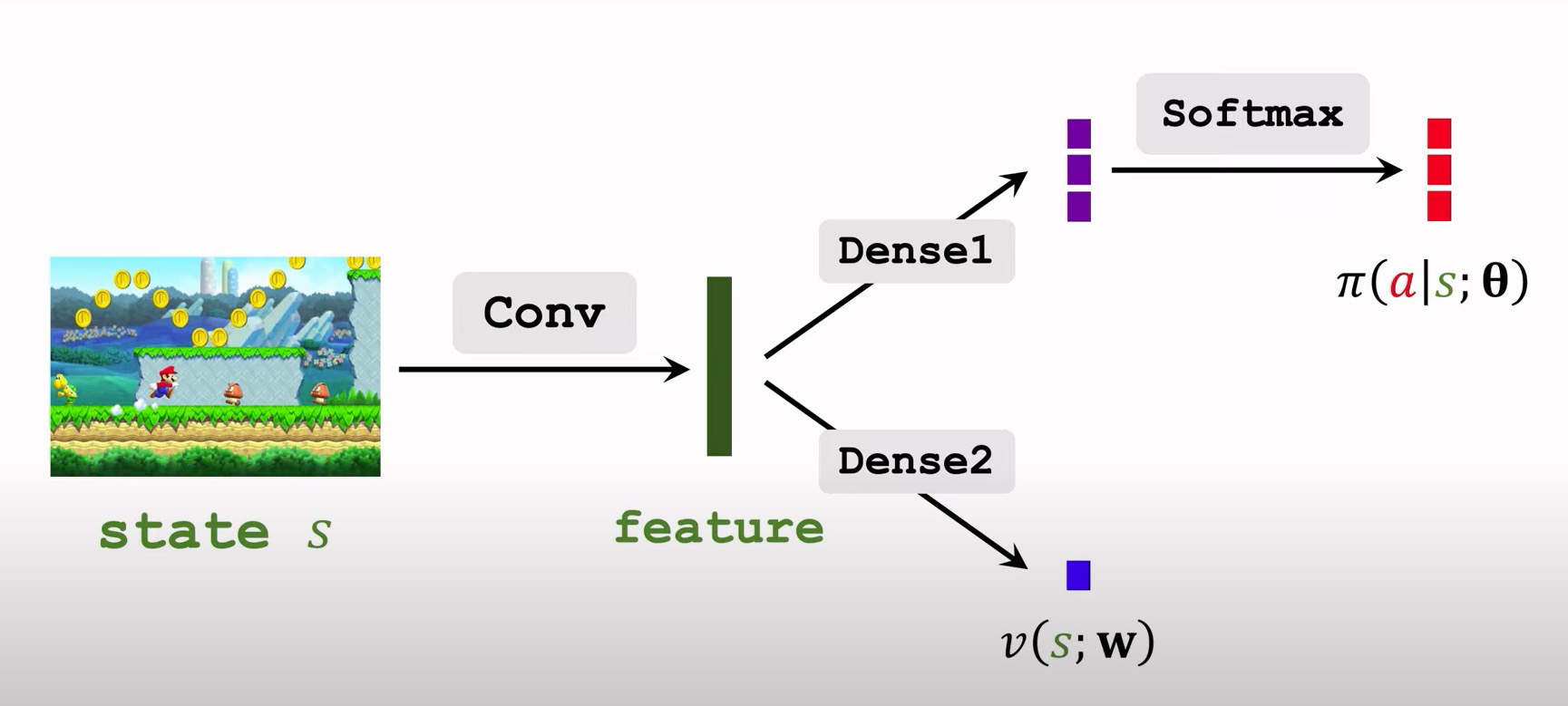

两个神经网络输入相同，都是用卷积层提取特征，所以可以共享卷积层。

使用REINFORCE来训练策略网络

使用梯度上升来更新策略梯度: $θ \leftarrow θ + β \cdot \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ} \cdot (u_{t} - v (s_{t}; w))$ 记$(u_{t}-v\left(s_{t} ; \mathbf{w}\right))$为 $-\delta_t$ 那么就有: $θ \leftarrow θ - β \cdot δ \cdot \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ}$

使用回归方法训练价值网络

预测误差:$\delta_t = v(s_t,w)-u_t$.
把$\delta_t^2$作为loss函数，求梯度: $\frac{\partial \delta_{t}^{2} / 2}{\partial \mathbf{w}}=\delta_{t} \cdot \frac{\partial v\left(s_{t} ; \mathbf{w}\right)}{\partial \mathbf{w}}$
梯度下降: $W \leftarrow W - α \cdot δ_{t} \cdot \frac{\partial v (s_{t}; w)}{\partial w}$

算法总结:

1.用策略网络$θ_{now}$控制智能体从头开始玩一局游戏，得到一条轨迹（trajectory）:
$s_1,a_1,r_1, s_2,a_2,r_2,…, s_n,a_n,r_n$
2.计算所有的回报:$u_t = \sum_{i=1}^n \gamma^{i-t} · r_i$.
3.让价值网络做预测:$\hat{u_t} = v(s_t;w)$
4.计算误差:$\delta_t = \hat{u_t} - u_t$
5.更新策略网络：

θ \leftarrow θ - β \cdot δ \cdot \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ}

6.更新价值网络：

W \leftarrow W - α \cdot δ_{t} \cdot \frac{\partial v (s_{t}; w)}{\partial w}

Advantage Actor-Critic(A2C)

同REINFORCE with Baseline 一样，有两个神经网络：

策略网络(actoe):$π(a|s;θ)$：用一个$π(a|s)$来近似，用来控制Agent。
价值网络(critic):$v(s;w)$：用一个状态价值函数$V_π(s)$来近似，用来评价状态s的好坏。他只依赖于状态s。

A2C的训练过程：

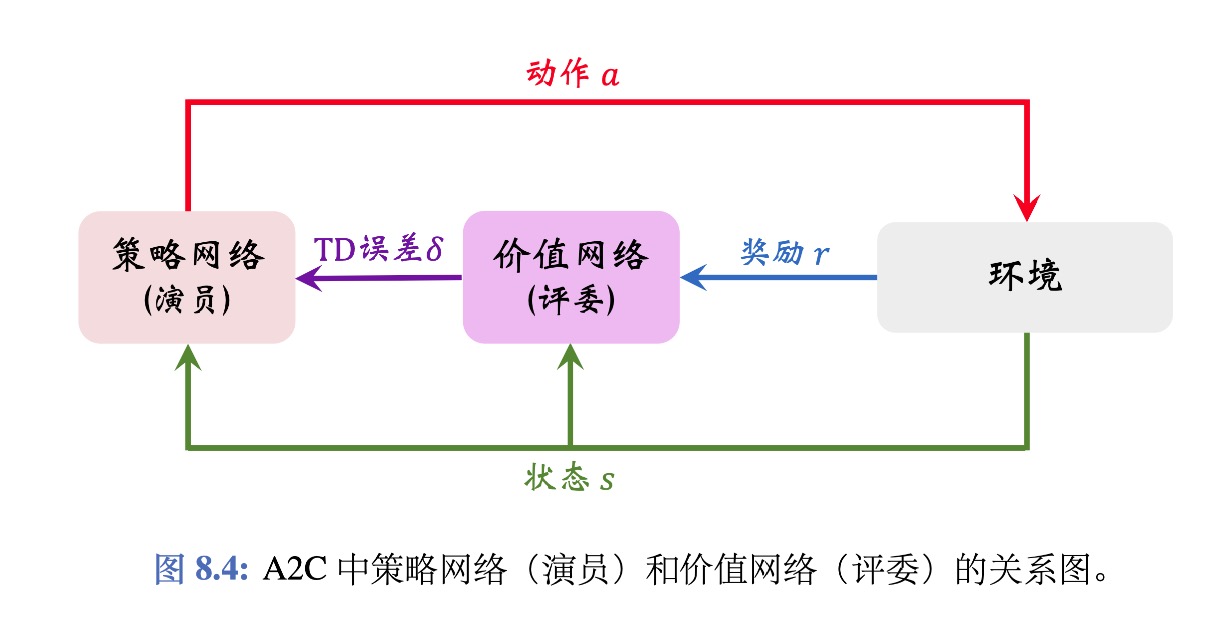
观测到一个transition$(s_t,a_t,r_t,s_{t+1}).$
TD target: $y_t = r_t + \gamma \cdot v(s_{t+1};w)$.
TD error: $\delta_t = v(s_t;w) - y_t$
更新策略网络(actor)：
$θ \leftarrow θ - β \cdot δ \cdot \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ}$
更新价值网络(critic)：
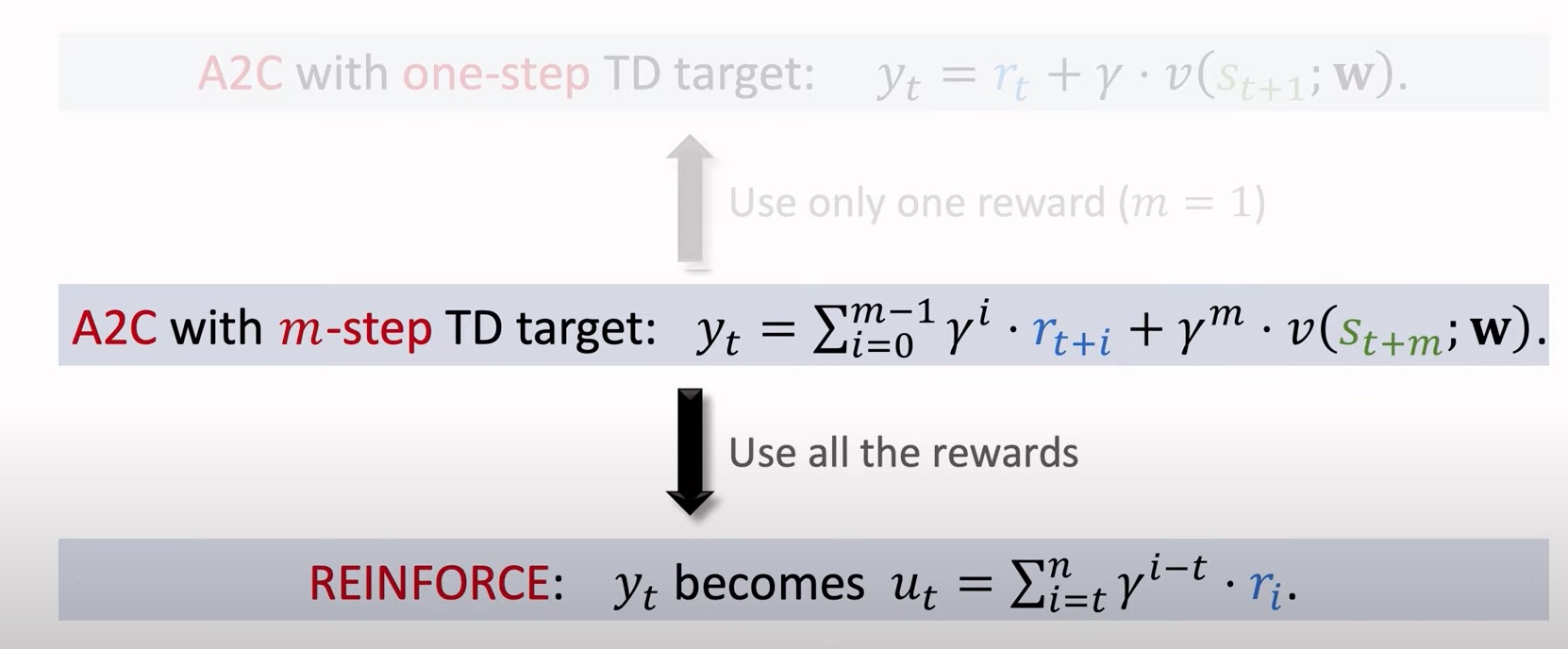
$W \leftarrow W - α \cdot δ_{t} \cdot \frac{\partial v (s_{t}; w)}{\partial w}$

One-Step VS Multi-Step Target

One-Step
- 一个transition$(s_t,a_t,r_t,s_{t+1})$.
- One-Step TD target:$y_t = r_t + \gamma \cdot v(s_{t+1};w)$.
Muti-Step
- 观测m个transition:${(s_{t+i},a_{t+i},r_{t+i},s_{t+i+1})}_{i=0}^{m=-1}$
  m-step TD target: $y_{t} = \sum_{i = 0}^{m - 1} γ^{i} \cdot r_{t + i} + γ^{m} \cdot v (s_{t + m}; w)$

Multi-Step 算法过程

观测到一个从t到t+m-1的轨迹
TD target: $y_{t}=\sum_{i=0}^{m-1} \gamma^{i} \cdot r_{t+i}+\gamma^{m} \cdot v\left(s_{t+m} ; \mathbf{w}\right)$.
TD error: $\delta_t = v(s_t;w) - y_t$
更新策略网络(actor)：
$θ \leftarrow θ - β \cdot δ \cdot \frac{\partial \ln π (a_{t} ∣ s_{t}; θ)}{\partial θ}$
更新价值网络(critic)：
$W \leftarrow W - α \cdot δ_{t} \cdot \frac{\partial v (s_{t}; w)}{\partial w}$

区别仅仅为更换了TD target，其他地方没有区别。

REINFORCE with Baseline与A2C的区别

用的网络完全一样，只是价值网络的功能有所区别。

A2C的价值网络为critic，用来评价Agent的表现。
REINFORCE with Baseline的价值网络用来当作Baseline，不会评价动作的好坏，唯一用途就是降低随机梯度造成的方差。

联系：

定义