[文献阅读]A Deep Reinforcement Learning based Offloading Game in Edge Computing 边缘计算中基于深度强化学习的卸载游戏

摘要与论文贡献

• CCF：A类
• 综合考虑通信开销和计算代价，将边计算中的任务卸载问题描述为每个时隙内的分散计算卸载博弈，并提出了一个能达到纳什均衡的算法来解决这一问题。
• 我们研究了无信息共享的卸货问题，并将其描述为多智能体POMDP问题。
  为了解决这一难题，提出了一种基于DRL和DNC的算法。

---

问题描述

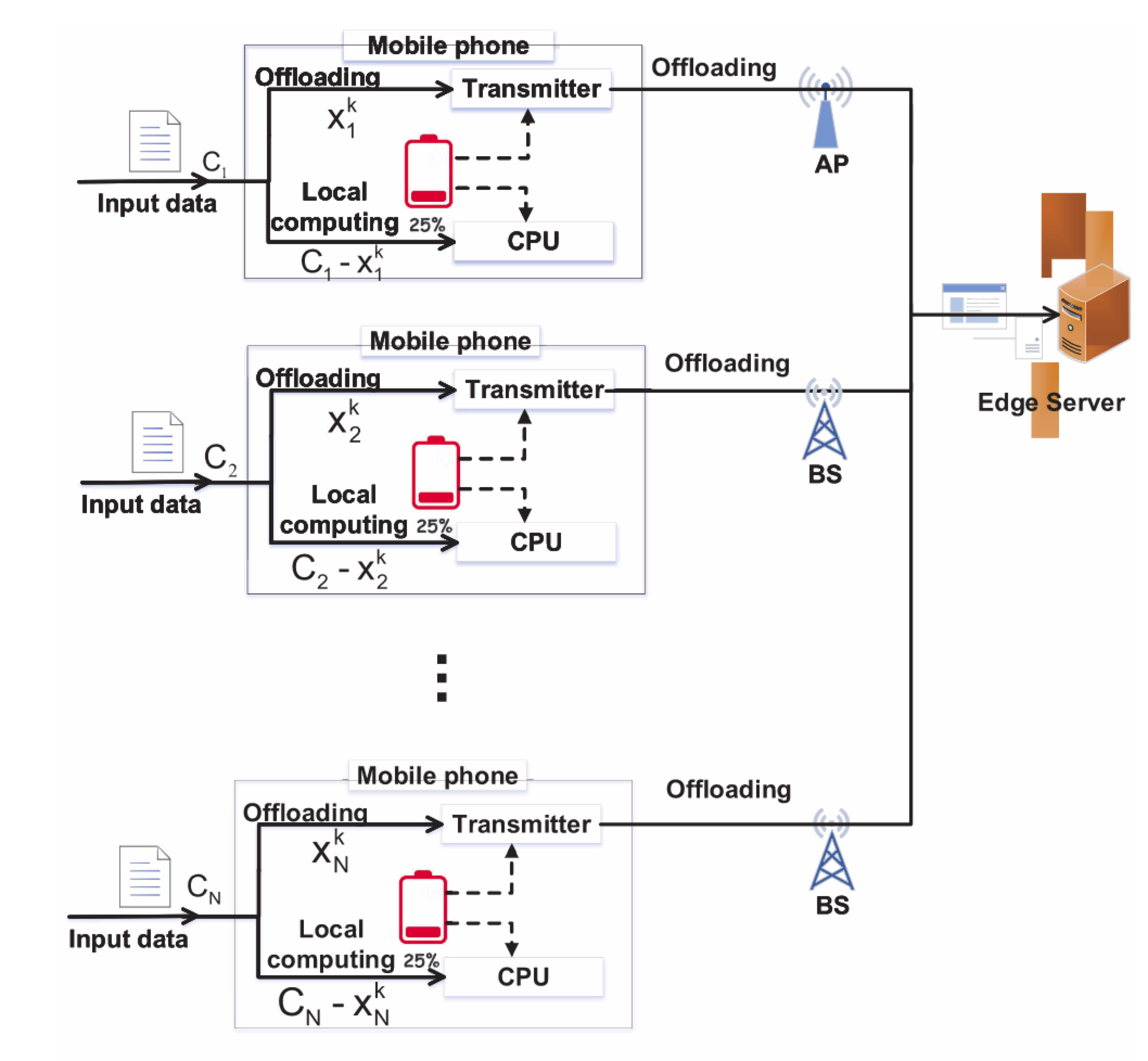
如图1所示，一共有N个用户，它们输入数据的总大小为$C_n$，用户n可以在时间k内卸载一部分的任务到边缘节点上，记为$x_n^k$,$b_n^k \in[\underline{B_n}, \bar{B_n}]$分别代表最小带宽和最大带宽。

边缘计算服务器采用深度学习等算法对输入数据进行处理。从所有用户卸载到边缘服务器的输入数据总量$\sum_{n=1}^{N} x_{n}^{k}$,让$R$表示为边缘服务器总共可用的资源。那么用户n可以获得边缘服务器资源为$\frac{x_{n}^{k}}{\sum_{m=1}^{N} x_{m}^{k}} R$,$F_n^k$表示为本地设备的计算能力。用户n在时间k内处理任务的时间为:

$$t_n^k=max\{\frac{x_n^k}{b_n^k}+\frac{\sum _{m=1}^N{x}_n^k}{R},\frac{C_n-x_n^k}{F_n^k}\}.$$

前半部分为传输时间+边缘服务器的计算时间，后半部分为在本地处理的时间。

用户n的传输带宽为$b_n^k$,$p_n$为用户n的基础传输成本。

定义用户n咋时间k内的效用函数为：

$$u_n(x_n^k,x_{-n}^k)=\frac{{\alpha }_n{x}_n^{k}R}{\sum _{m=1}^N{x}_m^k}-(p_n\frac{x_n^k}{b_n^k}+v_n(C_n-x_n^k))$$

n能得到的资源 - (传输能耗 + 用户处理本地数据的能耗)

其他用户的策略组$x_{-n}^k$，

寻找最大效用函数：

$$\begin{array}{rl}{\mathrm{O}\mathrm{P}}_{\text{User }}:& max{u}_n(x_n^k,x_{-n}^k)\\ & \text{ s.t. }{x}_n^k\in [0,C_n]\end{array}$$

目标是找到一个纳什均衡。

定义1.纳什均衡

当策略 $x^{k,\ast } = [x^{k,\ast}], n\in N$ ,满足以下条件时，达到纳什均衡:(3)

$$u_n(x_n^{k,\ast },x_{-n}^{k,\ast })\ge u_n(x_n^k,x_{-n}^{k,\ast })$$

---

算法与信息共享

研究了一种针对所有移动用户共享其全部信息的情况下的算法设计，包括权重$\alpha_n$、网络带宽$b_n$等。

定义2.给策略组$x_{-n}^k$，当n满足(4)

$$u_n(x_n^{k,\ast },{\mathit{x}}_{-n}^k)\ge u_n(x_n^k,{\mathit{x}}_{-n}^k)$$

达到最佳响应。

根据(3)和(4)，在纳什均衡条件下，所有用户都采用了最优的分流策略。基于最优响应的概念，我们有如下的观察

引理1

给定$x_{-n}^k$，且通信代价$\frac{p_{n}}{b_{n}}$大于计算代价$v_n$时，则第n个用户的卸载策略为：(5)

$$x_n^{k,\ast }=\{\begin{array}{ll}0,& \text{ if }{\mathrm{\Delta }}_1\\ C_n,& \text{ if }{\mathrm{\Delta }}_2\\ \sqrt{\frac{{\alpha }_n\sum _{m\ne n}^N{x}_m^k}{\frac{p_n}{b_n^k}-v_n}}R-\sum _{m\ne n}^N{x}_m^k,& \text{ otherwise }\end{array}where\begin{array}{rl}{\mathrm{\Delta }}_1& :\frac{{\alpha }_{n}R}{\frac{p_n}{b_n^k}-v_n}<\sum _{m\ne n}^N{x}_m^k,\text{ and }\\ {\mathrm{\Delta }}_2:C_n^2+{\left(\sum _{m\ne n}^N{x}_m^k\right)}^2\\ & +(2C_n-\frac{{\alpha }_{n}R}{\frac{p_n}{b_n^k}-v_n})\sum _{m\ne n}^N{x}_m^k<0,\end{array}$$

证明
根据效用函数对其求一阶导得：

$$\frac{\mathrm{\partial }{u}_n}{\mathrm{\partial }{x}_n^k}=\frac{{\alpha }_{n}R}{\sum _{m=1}^N{x}_m^k}-\frac{{\alpha }_{n}R{x}_n^k}{{\left(\sum _{m=1}^N{x}_m^k\right)}^2}-\frac{p_n}{b_n^k}+v_n$$

求二阶导得：

$$\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{x}_n^{k^2}}={\alpha }_n\frac{-2R\sum _{m\ne n}^N{x}_m^k}{{\left(\sum _{m=1}^N{x}_m^k\right)}^3}<0.$$

由于二阶导<0,所以这是一个凸函数，以你存在唯一纳什均衡。只需要当一阶导等于0时，就可以得到最佳响应。

$$\frac{\mathrm{\partial }{u}_n}{\mathrm{\partial }{x}_n^k}=\frac{{\alpha }_{n}R}{\sum _{m=1}^N{x}_m^k}-\frac{{\alpha }_{n}R{x}_n^k}{{\left(\sum _{m=1}^N{x}_m^k\right)}^2}-\frac{p_n}{b_n^k}+v_n=0$$

解得：

$${\tilde{x}}_n^k=\sqrt{\frac{{\alpha }_n\sum _{m\ne n}^N{x}_m^k}{\frac{p_n}{b_n^k}-v_n}R}-\sum _{m\ne n}^N{x}_m^k$$

当0< $\tilde{x_n^k}$ < $C_n$ 时，$x_n^{k,*}$ = $\tilde{x}_{n}^{k}$,如果<0，则全部在本地，其他则全部在边缘服务器上。

根据引理1，我们给出了下面的定理，供用户在纳什平衡点上决定他们的决策

定理1 在信息共享的情况下，用户在唯一纳什均衡下的计算卸载策略满足(10)

$$x_n^{k,\ast }=\frac{(N-1)R}{\sum _{m=1}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}}(1-\frac{(N-1)\frac{\frac{p_n}{k}-v_n}{{\alpha }_n}}{\sum _{m=1}^N\frac{\frac{b_m}{b_m^k}-v_m}{{\alpha }_m}})if\frac{((N-1)R-C_n)\sum _{m\ne n}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}}{(N-1)(N-2)R+C_n}<\frac{\frac{p_n}{b_n^k}-v_n}{{\alpha }_n}<\frac{\sum _{m\ne n}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}}{N-2}$$

证明:

根据(5)，当0<$x_b^{k,*}$<$C_n$时，

我们有(12)

$$\sum _{m=1}^N{x}_m^{k,\ast }=\sqrt{\frac{{\alpha }_n\sum _{m\ne n}^N{x}_m^{k,\ast }}{\frac{p_n}{b_n^k}-v_n}R}$$

(5)式是减去除自己之外的所有任务，这个全部加起来只需要去掉(5)后面的部分就行

设$ \Xi=\sum_{m=1}^{N} x_{m}^{k, *}$，根据(12)我们有(13)

$$x_n^{k,\ast }=\mathrm{\Xi }-\frac{{\mathrm{\Xi }}^2(\frac{p_n}{b_n^k}-v_n)}{R{\alpha }_n},$$ 因此 $$\mathrm{\Xi }=N\mathrm{\Xi }-{\mathrm{\Xi }}^2\sum _{m=1}^N\frac{\frac{p_m}{b_m^k}-v_m}{R{\alpha }_m}$$

由于$x_n^{k,*} \in $(0,$C_n$),因此$\Xi$ > 0是(14)独一无二的解，我们获得了一个独一无二的$\Xi$：

$$\mathrm{\Xi }=\frac{(N-1)R}{\sum _{m=1}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}}$$

带入(13)得到(10),因此计算卸载博弈存在唯一的纳什均衡。

总之通过了一大串的计算证明了纳什均衡的唯一性和知道了何时达到纳什均衡，即式(10)。

讨论根据定理1，边缘服务器的计算资源、每个用户的传输成本、每个用户的无线带宽、每个用户的本地计算成本以及用户对延迟和能量消耗的偏好决定了纳什均衡下每个用户的卸载策略

推论 在信息共享的情况下，如果第n个用户的电池电量不足，将较少的计算负载转移到边缘服务器

证明
如果用户n的电池电量不足。为了节省能源，用户希望在计算卸载决策时将更多的能量消耗放在更高的权重上。根据(10)计算$\alpha _n$的一阶导（*）

$$\frac{\mathrm{\partial }{x}_n^{k,\ast }}{\mathrm{\partial }{\alpha }_n}=\frac{(N-2)\frac{\frac{p_n}{b_n^k}-v_n}{{\alpha }_n}\sum _{m=1}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}}{{\alpha }_n{}^2{\left(\sum _{m=1}^N\frac{\frac{p_m}{b_m^k}-v_m}{{\alpha }_m}\right)}^3}$$

因为 $x_n^{k,*}$，我们可以推断此导数大于0（中间推断过程详看论文）。因此，当用户的电池处于低电量时，它将减轻权重$\alpha _n$，减少边缘服务器的计算负荷。

本文提出了一种能够实现完全信息共享的纳什均衡的算法1。如算法1所示，在每个时间段，每个用户首先与其他用户共享自己的信息。然后每个用户从他人那里接收到这个私有信息，根据定理1可以得到的最优计算卸载策略来决定自己的卸载策略。

个人小结：（10）式用来寻找纳什均衡，即应该卸载多少到边缘服务器上，（*）式用来寻找权重

---

没有信息共享的算法

在实践中，我们很难知道其他用户的各种信息，所以提出了一种将动态分散计算卸载博弈描述为多智能体部分可观测的马尔可夫决策过程，设计了一种新的基于多智能体DRL方法的用户动态计算卸载算法D-DRL。
使用该算法，每个用户可以直接从游戏历史中确定近似最优的计算卸载策略，而不需要任何关于其他用户的先验信息。

部分可观测的马尔可夫决策过程

马克洛夫决策过程

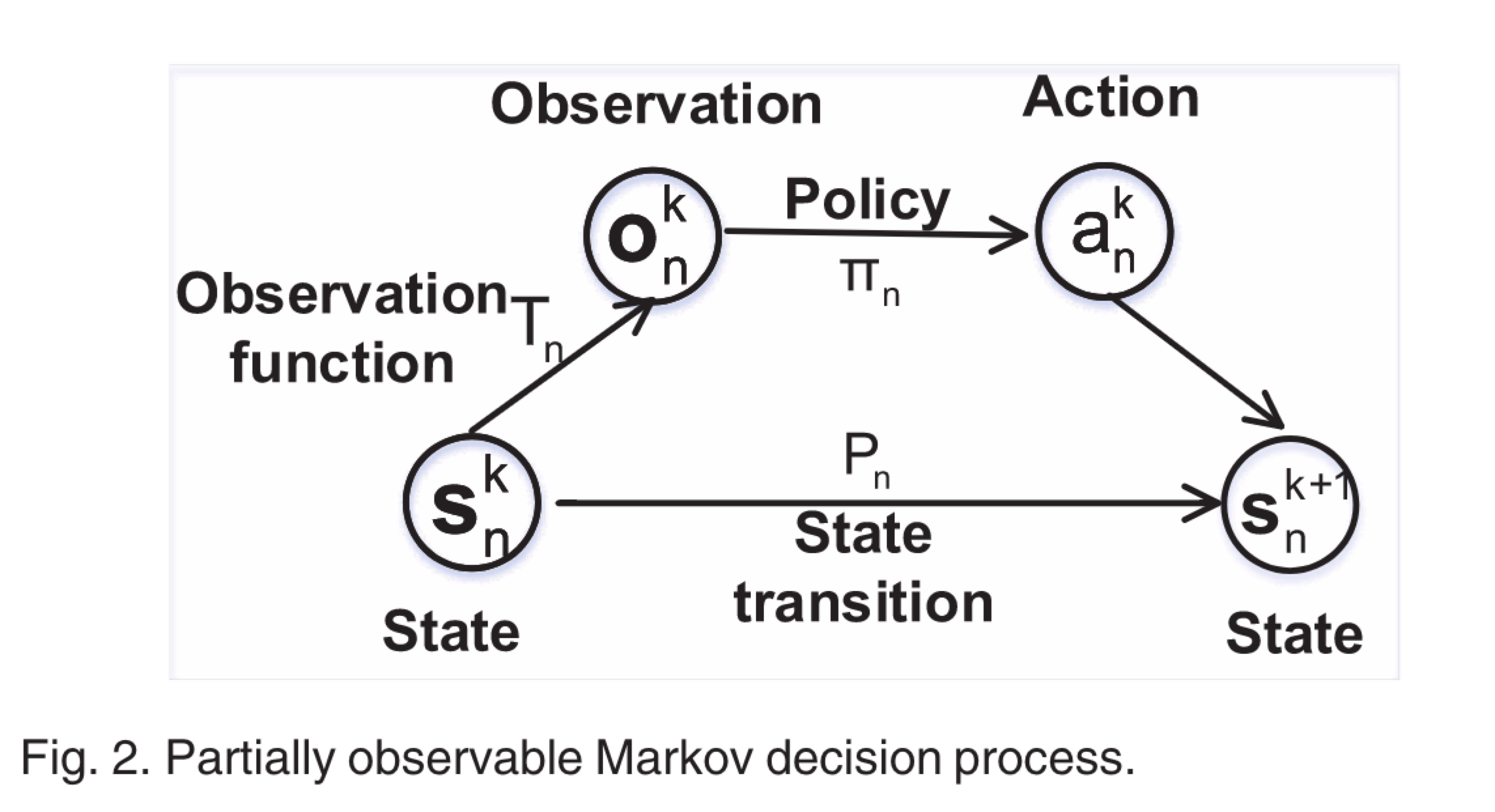
可以被表示为$M_p$ = ,一个持续的状态空间 S = {$s_n^k$|$\forall k \in \mathbb{N} $},一个行动空间 A = {$a_n$},n $\in$ N,一个状态转移概率函数 P = {$P_n : S_n · A · S_n \longrightarrow [0,1]$}, n $\in$ N,一个奖励空间 R = {$R_n$}, n $\in$ N ,一个观测空间O和一个观测函数T = {$T_n : S_n · O_n \longrightarrow [0,1]$} ,n $\in$ N。状态空间S是部分可知的，决策依据是观测空间O。用户只能管擦过去的策略${ x^{K-L},x^{K-L+1},…,x^{K-1} }$和它们自己的属性。为这个游戏建立如下POMDP:

Observation Space： 这里有一个观测空间 O = {$O_n$},n $\in$ N,$O_n$ = {$o_n^k$|$\forall k \in \mathbb{N} $}}和$O_n^k$ = $ [ s x^{K-L}_ {-n },b^{K-L+1}_ {n},…,x^{K-1} _ {-n},b^{K}_ {n}] ,其中 x^{K-L}_{-n} $是随机生成的 k <= L。在时隙k开始时，对用户n的观测包括其在前L-1个时隙和当前时间的无线电带宽，以及其他用户在前L个时隙上传的输入数据的大小。

Action Space： A = {$A_n$,},n $\in$ N, $A_n$ = {$\forall k \in \mathbb{N} $},在时隙k开始时,用户n的动作是加载到边缘服务器输入数据的大小$x_n^k$。

Observation Transition: 当所有用户在时间k采取行动后，用户的观测 将过渡到$o_n^{k+1}$ 满足

$${\mathit{o}}_n^{k+1}\sim {\int }_{{\mathcal{S}}_n}{T}_n(\cdot \mid s_n)P_n(s_n\mid s_n^k,{\left\{x_m^k\right\}}_{m\in \mathcal{N}})\mathrm{d}{s}_n$$

从$b_n^k$到$b_n^{k+1}$的转变是一个随机过程。因此，整个观测转换过程是随机的。

Reward Space： R = {$R_n$,},n $\in$ N, $R_n$ = {$\forall k \in \mathbb{N} $} 和 $r_n^k$ = $u_n$($x_n^k,x_{-n}^k$).当所有用户在时间k采取行动后，每个用户将根据其效用函数计算其奖励，然后开始下一个游戏。

Multi-Agent Learning Objective： 我们使用来描述了用户n参数化$\theta_n$ 的计算卸载策略$\pi_{\theta_n}$，$\pi_{\theta_n}$ : $O_n$ x $A_n \longrightarrow[0,1]$,然后在此基础上，给出了用户的策略优化问题:(17)

$$\begin{array}{rl}{\mathit{\theta }}_n^{\ast }& =\arg \underset{{\mathit{\theta }}_n}{max}{L}_n\left({\pi }_{{\mathit{\theta }}_n}\right)\\ & =\arg \underset{{\mathit{\theta }}_n}{max}\mathbb{E}[V^{{\pi }_{{\mathit{\theta }}_n}}\left({\mathit{o}}_n^0\right)\mid {\rho }_n^0]\\ & =\arg \underset{{\mathit{\theta }}_n}{max}\mathbb{E}[Q^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n^0,x_n^0)\mid {\rho }_n^0,{\pi }_{{\mathit{\theta }}_n}]\end{array}$$

where

$$\begin{array}{rl}{V}^{{\pi }_{{\theta }_n}}\left({\mathit{o}}_n\right)& =\mathbb{E}[R_n^k\mid {\mathit{o}}_n^k={\mathit{o}}_n,\mathrm{\Pi },\mathcal{P},\mathcal{T}]\\ Q^{{\pi }_{{\theta }_n}}({\mathit{o}}_n,x_n)& =\mathbb{E}[R_n^k\mid {\mathit{o}}_n^k={\mathit{o}}_n,x_n^k=x_n,\mathrm{\Pi },\mathcal{P},\mathcal{T}]\\ R_n^k& =\sum _{l=k}^K{\gamma }^{l-k}{r}_n^k\end{array}$$

$\Pi = {\pi_{\theta_n}}$,${n \in \mathcal{N}}$，表示所有用户的策略集。$V^{\pi_{\theta_n}}$是观测价值函数。$Q^\pi_{\theta_n}$($o_n,x_n$)是当前观测的动作价值函数，$\rho_n^0$是用户n的初试观测概率分布，$R_n^k$是用户在时间k内的预期未来汇报$\gamma \in $[0,1]是折扣率。

因此，在将动态分散计算卸载博弈描述为多智能体POMDP后，在非合作场景下，可以通过多智能体策略梯度DRL方法来优化用户的计算卸载策略

---

算法设计

综述

如图3所示，有N个用户，每个用户都有一个称为DRL控制器的模块，该模块确定上传到边缘服务器的输入数据的大小

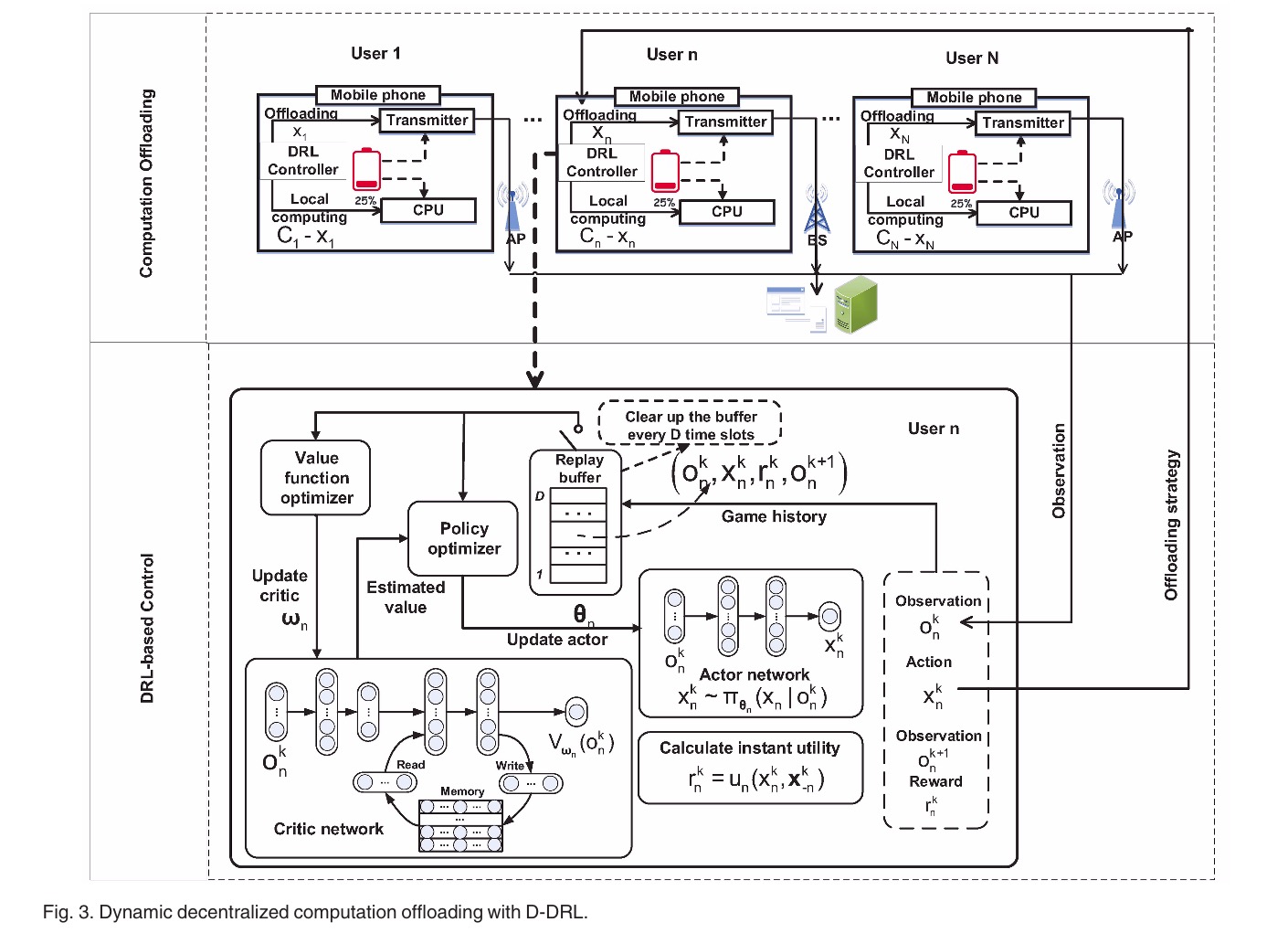
其中包括动作网络、价值网络、Replay Buffer、效用计算模块、内存模块、值函数优化器和策略优化器。具体地说，动作网络直接通过多个完全连接的神经网络输出根据观察到的动作。价值网络首先将观测值映射到特征向量中，然后从记忆中读取特征，通过组合这些特征可以得到最终的观测值，并通过写操作来更新其记忆。每个时隙开始时，都会清空replay buffter。

动作网络与价值网络的设计

由于用户无法分享它们观测到的数据，因此为每个用户设计了一个分散的动作网络和分散的价值网络。用户n的策略的动作网络近似为$\pi_{\theta_n}$,价值函数的价值网络近似为$V_{\omega_n}$,$\theta_n$与$\omega_n$分别为动作网络和价值网络的模型参数。

更准确的说，动作网络$\pi_{\theta_n}$被设计成多层全连接的神经网络，它从用户的实时观测数据$o_n^k$中确定用户n上传的输入数据$x_n^k$的大小。价值网络$V_{\omega_n}$更为复杂，它由连接层和DNC组成。DNC是一种特殊的递归神经网络，具有内部记忆模块，能够学习和记忆输入的过去隐藏状态。在DNC中，$V_{\omega_n}$估计的观测值取决于整个观测历史。带有DNC的价值网络可以使用户更快更好地收敛到均衡状态。并且在解决POMDP问题上是有效的。

策略优化方法

通过策略梯度法对每个用户的连续策略进行优化，其目标函数定义在(17)中。根据[37]中证明的策略梯度定理和[38]中提出的信赖域策略优化理论，可以计算出策略梯度为

$$\begin{array}{rl}{\mathrm{\nabla }}_{{\mathit{\theta }}_n}{L}_n& ={\mathbb{E}}_{{\pi }_{{\mathit{\theta }}_n},{\rho }_n^1\left({\mathit{o}}_n\right)}[{\mathrm{\nabla }}_{{\mathit{\theta }}_n}\log {\pi }_{{\mathit{\theta }}_n}({\mathit{o}}_n,x_n)Q^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n,x_n)]\\ & ={\mathbb{E}}_{{\pi }_{{\mathit{\theta }}_n},{\rho }_n^1\left({\mathit{o}}_n\right)}[{\mathrm{\nabla }}_{{\mathit{\theta }}_n}\log {\pi }_{{\mathit{\theta }}_n}({\mathit{o}}_n,x_n)A^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n,x_n)]\\ & \approx {\mathbb{E}}_{{\pi }_{{\hat{\mathit{\theta }}}_n},{\rho }_n^1\left({\mathit{o}}_n\right)}[f_n{\mathrm{\nabla }}_{{\mathit{\theta }}_n}\log {\pi }_{{\mathit{\theta }}_n}({\mathit{o}}_n,x_n)A^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n,x_n)]\end{array}$$

where

$$f_n=\frac{{\pi }_{{\theta }_n}({\mathit{o}}_n\mid x_n)}{{\pi }_{{\hat{\theta }}_{\mathit{\theta }}}({\mathit{o}}_n\mid x_n)},A^{{\pi }_{{\theta }_n}}({\mathit{o}}_n,x_n)=Q^{{\pi }_{{\theta }_n}}({\mathit{o}}_n,x_n)-V^{{\pi }_{{\theta }_n}}\left({\mathit{o}}_n\right)$$

是观测和动作的优势函数。$\hat{\theta_n}$表示采样的策略参数，$\rho_n^1$ ($o_n$)是POMDP引起的观测分布,为了加快策略优化的收敛速度，我们采用了[39]中提出的最近策略优化(PPO)方法，该方法将策略梯度剪裁为

$${\mathrm{\nabla }}_{{\mathit{\theta }}_n}{L}_n\approx {\mathbb{E}}_{{\pi }_{{\hat{\mathit{\theta }}}_n},{\rho }_n^1\left({\mathit{o}}_n\right)}[{\mathrm{\nabla }}_{{\mathit{\theta }}_n}\log {\pi }_{{\mathit{\theta }}_n}({\mathit{o}}_n,x_n)C({\mathit{o}}_n,x_n)]$$

where

$$C({\mathit{o}}_n,x_n)=min[f_n{A}^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n,x_n),\eta \left(f_n\right)A^{{\pi }_{{\mathit{\theta }}_n}}({\mathit{o}}_n,x_n)]$$ $$\eta (x)=\{\begin{array}{ll}1+\epsilon ,& x>1+\epsilon \\ x,& 1-\epsilon \le x\le 1+\epsilon \\ 1-\epsilon ,& x<1-\epsilon \end{array}$$

$\varepsilon$是一个可调参数。

动作和价值网络的更新规则

定义用于更新价值网络的损失函数

$$J_n\left({\mathit{\omega }}_n\right)={\mathbb{E}}_{{\mathit{o}}_n\sim {\rho }_n^1\left({\mathit{o}}_n\right)}{[-V_{{\mathit{\omega }}_n}\left({\mathit{o}}_n\right)+{\mathbb{E}}_{{\mathit{o}}_n^{\mathrm{\prime }},x_n}[r+V_{{\mathit{\omega }}_n}\left({\mathit{o}}_n^{\mathrm{\prime }}\right)]]}^2,$$ $o_n^,$是用户n下一时刻的状态，在训练过程期间，模拟梯度$\omega_n$计算为(26) $${\mathrm{\nabla }}_{{\mathit{\omega }}_n}{\hat{J}}_n=\frac{1}{D}\sum _{k=0}^{D-1}[V_{{\mathit{\omega }}_n}\left({\mathit{o}}_n^k\right)-Y_n^k)]\frac{d{V}_{{\mathit{\omega }}_n}\left({\mathit{o}}_n\right)}{d{\mathit{\omega }}_n}$$

where

$$Y_n^k=R_n^k-{\gamma }^{D-k}{R}_n(D)+{\gamma }^{D-k}{V}_{{\omega }_n}({\mathit{o}}_n(D))$$

D是用于更新价值网络的小批量大小。通过小批量随机梯度下降法进行更新如下(28)

$${\mathit{\omega }}_n\leftarrow {\mathit{\omega }}_n-l_{n,1}{\mathrm{\nabla }}_{{\mathit{\omega }}_n}{\hat{J}}_n$$

$l_{n, 1}$是学习率，

此外，模拟梯度$\theta_n$的计算为(29)

$${\mathrm{\nabla }}_{{\mathit{\theta }}_n}{\hat{L}}_n=\frac{1}{D}\sum _{k=0}^{D-1}{\mathrm{\nabla }}_{{\mathit{\theta }}_n}\log {\pi }_{{\mathit{\theta }}_n}({\mathit{o}}_n^k,x_n^k)C({\mathit{o}}_n^k,x_n^k)$$

D是用于更新动作网络的小批量大小，更新动作网络$\pi_{\theta_n}$用小批量随机梯度上升如下(30)

$${\mathit{\theta }}_n\leftarrow {\mathit{\theta }}_n+l_{n,2}{\mathrm{\nabla }}_{{\mathit{\theta }}_n}{\hat{L}}_n$$

$l_{n,2}$是用户n的学习率

算法

伪码如算法2所示，每个用户初始化他们的观察和他们的动作网络和价值网络的参数(行1-3)。

在每个时隙k，每个用户观察它的带宽并更新它的观察(行6)。然后，每个用户将其输出的观察、策略、奖励和新的观察存储到其回放缓冲区中(第7行)。接下来，每个用户将其当前观测值作为其动作网络的输入，然后将其输入数据的一部分上传到边缘，并严格根据动作网络的输出（第8行）。在所有用户上传数据后，每个用户计算其即时效用(奖励)(第9行)。
每个用户在每个时间段更新其动作和价值网络(第13行)。他们将重放缓冲器中的数据记录作为一个小批量，并估计更新动作和价值网络的梯度(第14行)。在此之后，每个用户分别通过小批量随机梯度上升和下降方法多次优化其动作和价值网络(第15行)。最后，清除重放缓冲区(第18行)。

论文地址

Zhan, Yufeng, et al. “A deep reinforcement learning based offloading game in edge computing.” IEEE Transactions on Computers 69.6 (2020): 883-893.