[文献阅读] Deep Reinforcement Learning-based Task Offloading in Satellite-Terrestrial Edge ComputingNetworks 星地边缘计算网络中基于深度强化学习的任务分流

摘要与主要贡献

• CCF：C类

缩写
地面云（TC），基于任务卸载饿深度强化学习(DRTO)，卫星边缘计算（SatEC），深层神经网络（DNN）

考虑一个SatEC，将卸载费用建模为带宽和能量消耗的加权和。以最小化卸载成本为目标，将卸载位置决策和带宽分配问题转化为MIP问题。将卸载位置决策和带宽分配问题转化为MIP问题。

论文贡献

• 卫星-地面协同卸载。将卸载位置的决策和带宽分配问题归纳为MIP问题
• 无模型学习。所提出的DRTO算法只根据当前的通道状态进行卸载决策。同时，DRTO可以通过学习信道状态的实时趋势来改进其卸载策略，以适应卫星-地面网络的高动态。
• 低时间复杂度。与传统的优化方法相比，DRTO完全不需要解决硬MIP问题。此外，我们还动态调整动作空间的大小，以加快学习过程。

---

系统模型与问题描述

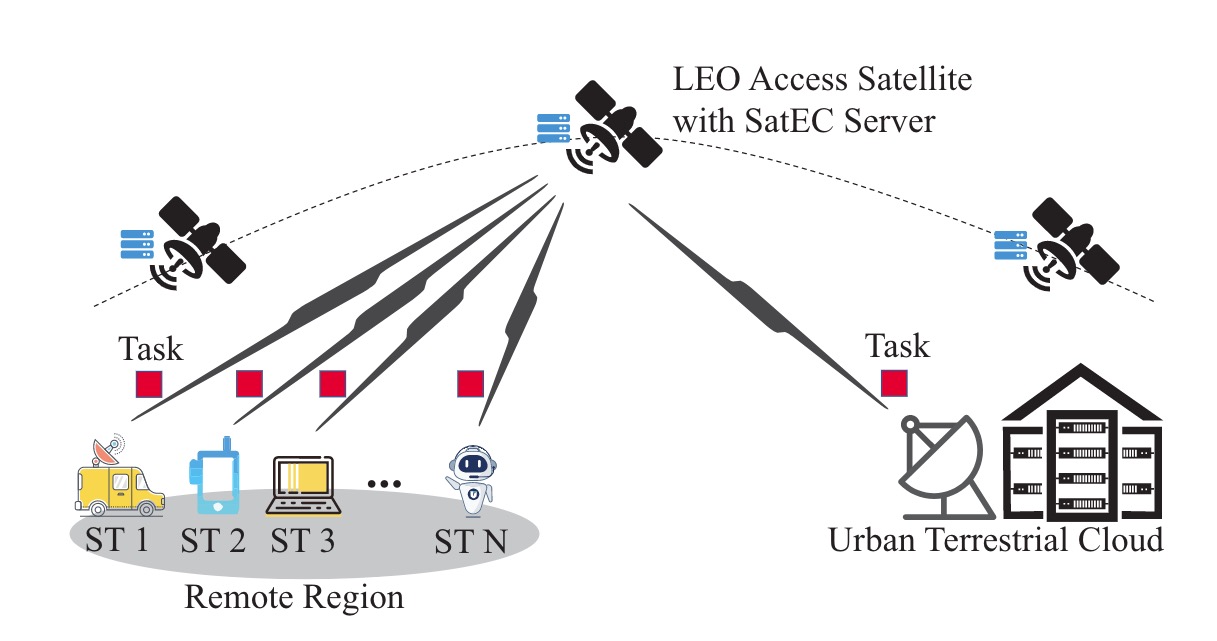
如图1所示，LEO设备在地球表面高速飞行，并将ST（边缘设备）远程连接到地面站，TC通过光纤与地面站链接，传输时延可以忽略不计。
假定接入卫星总是可用的（不考虑间歇性通信？），并考虑N={1,2,…,N}个ST设备和一个TC在同一介入卫星的覆盖范围内。

为方便，从ST到卫星称为第一跳，从卫星到TC称为第二跳。论文中的符号如下表所示

符号	解释
$x_n$	第n个ST设备的卸载位置（1表示在SatEC，0表示在TC）
$α_nB$	第n个ST的带宽
$α_{N+n}B$	分配给第n个ST的任务转发的带宽
B	接入卫星的总带宽
$P_n$	第n个ST的传输能耗
$P_{Sat}$	接入卫星的传输能耗
$h_n$	第n个ST与卫星之间的信道增益
$h_{TC}$	接入卫星与ST之间的信道增益
$N_0$	接收器的噪声功率
L	任务大小
k	计算强度
$f_1$	SatEC服务器的CPU频率
$f_0$	TC的CPU频率
$p_c$	SatEC服务器的计算能力消耗
λ	延迟-能量权重参数

卸载位置

对于第n个ST卸载的任务，其接入卫星可以选择本地处理或透明地转发到其连接的TC。我们定义第n个ST为$x_n$，$x_n$ = 1表示卸载到卫星，$x_n$ = 0表示卸载到TC。

卸载花费

主要取决于延迟和能耗，卸载到不同位置的成本不同，定义如下

卸载到SatEC

其主要开销包括传输开销和计算开销。$α_n$为第n个ST的带宽比例，然后第n个ST的第一跳传输数率公式如下

$C_{1,n}$ = $α_n$B$log_2$(1+$p_nh_n/N_0$)

香农公式：C = B$log_2$(1 + S/N) . C为（最大）传输速率，B为带宽，S为平均功率，N为信道内噪声功率。

B代表接入卫星的总带宽。$P_n$为第n个ST的传输能耗，$h_n$为第n个ST与卫星之间的信道增益，$N_0$代表接收器的噪声功率。

基于第一跳的传输功率$C_{1,n}$，传输延迟为$T_{1,n}$ = L/$c_{1,n}$,L为任务数据大小。第n个ST的能耗为$E_{1,n}$ = $p_nT_{1,n}$

忽略排队延迟，SatEC服务器的计算延迟为$T_{1,n}^c$ = KL/$f_1$,k代表任务的计算强度（周期/比特为单位），$f_1$为卫星的CPU频率（周期/s为单位）。用于计算的能耗为$E_{1,n}^c$ = $p_cT_{1,n}^c$,$p_c$为计算能耗。

第n个ST的总延迟和总能耗为

$T_n^{Sat}$ = $T_{1,n}$ + $T_{1,n}^c$ , $E_n^{Sat}$ = $E_{1,n}$ + $E_{1,n}^c$

传输延迟+卫星的计算延迟，传输能耗+卫星的计算能耗

卸载到TC

出了ST的传输成本外，还应该包括卫星的转发成本和TC的计算成本。

$α_{N+n}$为第n个ST任务转发分配的带宽比例。第二跳的成本为$C_{2,n}$ = $α_{N+n}$B$log_2$(1+$P_{Sat}h_{TC}/N_0$),$P_{Sat}$表示卫星的传输消耗，$h_{TC}$表示接入卫星与TC之间的通道增益。

ST的感知延迟和能耗为
$T_{2,n}$ = L/$C_{2,n}$,$E_{2,n}$ = $P_{Sat}$$T_{2,n}$

TC的计算延迟为$T_{2,n}^c$ = kL/$f_0$,$f_0$为TC的CPU计算频率，由于TC持续供电，所以忽略TC的能耗

总延迟和总能耗为

$T_{1,n}^{TC}$ =$T_{1,n}$ + $T_{2,n}$ + $T_{2,n}^c$,$E_n^{TC}$ = $E_{1,n}$ + $E_{2,n}$

问题描述

卸载成本最小化问题的表达如下：

P为一个混合整数规划问题，其中0-1变量于连续变量α是相互耦合的

为了解决问题，本文提出了一种基于深度强化学习的任务卸载算法。具体地说采用了一个DNN来映射当前的通信状态到卸载位置，并通过增强学习来改进DNN。

---

DRTO算法

设计一个最小卸载算法π：$ h \to x^\ast $ ，他会快速选择最佳的卸载位置 $x^\ast= [x_1^\ast,x_2^\ast,…,x_N^\ast] $ ,仅基于当前通信状态$h = [h_1,h_2,..,h_N,h_{TC}] $。

算法框架如下图所示

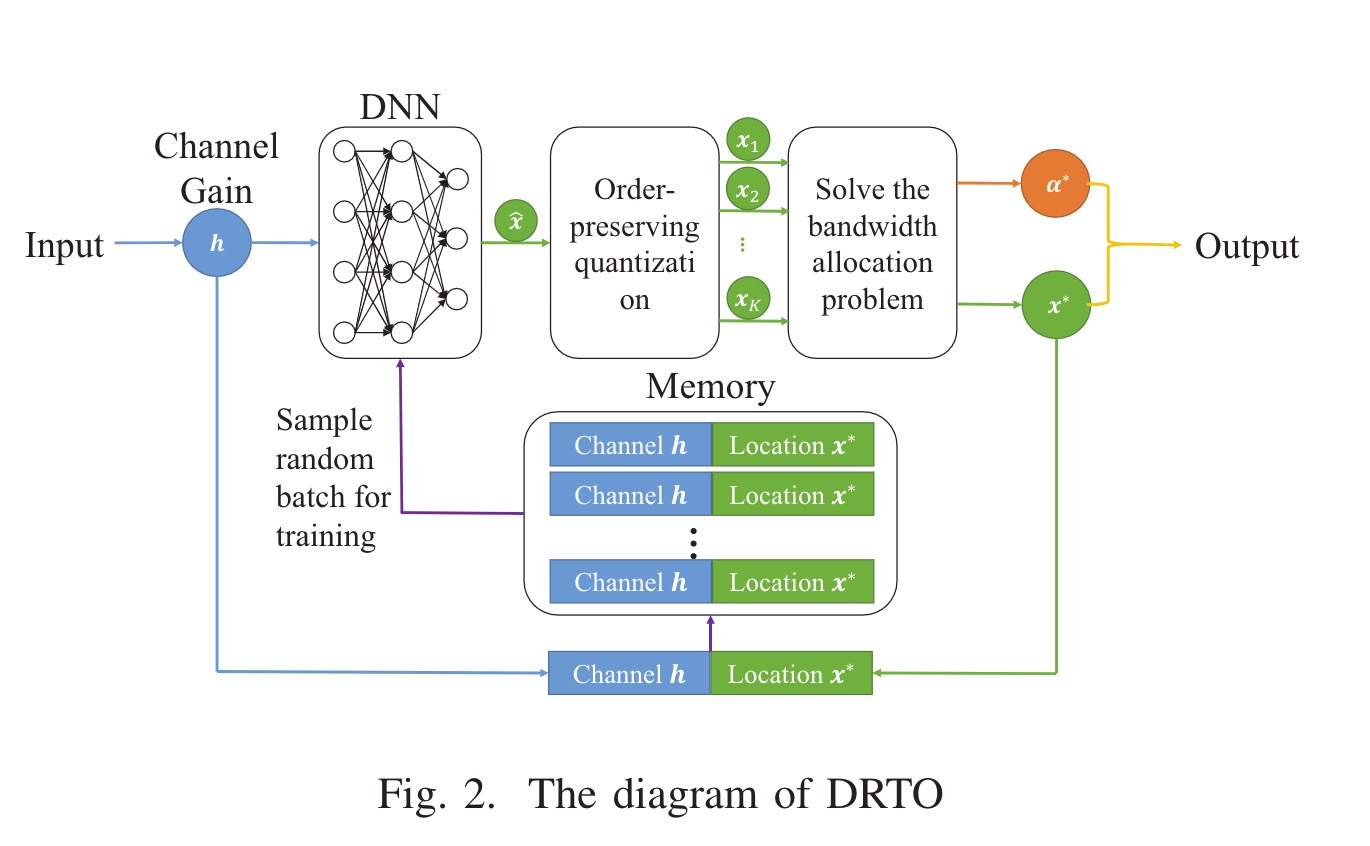
首先DNN获取当前通道h的输入和生成卸载位置$\hat{x}$,然后我们将松弛位置$\hat{x}$量化为k个二进制卸载策略，$x_1,x_2,..x_K$。最佳位置$x^\ast$是通过一系列的带宽分配凸性问题得到的。随后将新获得的通信状态卸载位置对（h,$x^\ast$）添加到重放存储器中。将从存储器中随机采样一批数据，以改善每个δ时间帧的DNN。
为了进一步减少运行时的消耗，我们动态调整K来加快学习过程。

DRTO的算法如下

生成卸载地点

如图2上半部分所示。在每个时间帧内，完全连接的DNN获取当前通道的输入，并生成卸载位置$\hat{x}$ = [$\hat{x_1},\hat{x_2},…,\hat{x_N}$],$\hat{x}$被量化为k个策略，在给定候选策略k的情况下，DRTO算法根据最小的卸货成本选择最优的卸货地点$x_∗$

由于通用逼近定理[22]，采用完全连通的DNN来逼近这种映射。
DNN的特征是连接隐含神经元的权值，共四层，即输入层、两个隐藏层和输出层。
在这里，我们分别在隐层和输出层使用ReLU和Sigmoid激活函数，从而输出松弛卸货位置的每个入口都满足$\hat{x}_n \in $ (0,1)。

然后，$\hat{x}$量化为k个二进制卸载策略，K $\in$ [1,$2^N$]。

对于每个量化策略$x_k$ = [$x_{k,1},x_{k,2},…,x_{k,N}$]，$x_{k,n}$ <= $x_{k,m}$,应有$\hat{x}_n$ <= $\hat{x}_m$, n,m$\in${1,2,…,N}。

个人理解：将$\hat{x}$ = [$\hat{x_1},\hat{x_2},…,\hat{x_N}$]量化成k个不同的卸载策略，然后通过比较这k个策略，选出最好的策略。$x_n$的意思为第n个策略，$x_{k,1}$表示第k个策略中第1个设备选择的卸载位置。而$\hat{x}$由h决定。

1）第一个量化的位置每个ST的卸载位置由下式给出

$$x_{1,n}=\{\begin{array}{ll}1& {\hat{x}}_n>0.5,\\ 0& {\hat{x}}_n\le 0.5.\end{array}n=1,2,\dots ,N$$

2)对于剩余的k-1个卸载策略，首先对$\hat{x}$的每个条目按照它们到0.5的距离进行排序，例如

$$|{\hat{x}}_{(1)}-0.5|\le |{\hat{x}}_{(2)}-0.5|\le \dots \le |{\hat{x}}_{(N)}-0.5|$$

$\hat{x}_{(n)}$表示排序后的第n个条目。之后，第k个卸载位置$x_k$，k = 2,3,…,K由下式给出

$$x_{k,n}=\{\begin{array}{ll}1& {\hat{x}}_n>{\hat{x}}_{(k-1)},\\ 1& {\hat{x}}_n={\hat{x}}_{(k-1)}\text{ and }{\hat{x}}_{(k-1)}\le 0.5,\\ 0& {\hat{x}}_n={\hat{x}}_{(k-1)}\text{ and }{\hat{x}}_{(k-1)}>0.5,\\ 0& {\hat{x}}_n<{\hat{x}}_{(k-1)}.\end{array}$$

我们得到了k个候选卸载地点，给一个固定的卸载位置$x_k$，原始的卸货费用最小化问题P被转化为一个凸问题α

$$\begin{array}{c}{\mathcal{P}}^{\mathrm{\prime }}:\underset{\mathit{\alpha }}{min}F({\mathit{x}}_k,\mathit{\alpha })\\ \text{ s.t. }0\le \sum _{n=1}^{2N}{\alpha }_n\le 1\end{array}$$

保序量化理解过程
原文连接[1]

这个问题可以用CVXPY[21]这样的凸优化工具来求解。在给定$x_k$的情况下，我么可以的到最优带宽分配$α^∗_{x_k}$和最小卸载费用F($x_k$,$α^∗_{x_k}$)，反复求解问题$p^,$,通过以下式子得到最佳卸载位置

$${\mathit{x}}^{\ast }=\arg \underset{\left\{{\mathit{x}}_{\mathit{k}}\right\},k=1,2,\dots K}{min}F({\mathit{x}}_k,{\mathit{\alpha }}_{{\mathit{x}}_k}^{\ast })$$

以及最优带宽分配$α^∗$。

这个最优化问题看得不是很明白。

更新卸载策略

DRTO的训练样本由最新的信道状态h和卸载位置$x^\ast$组成。当前的卸载策略是根据上一时间帧生成的，因此相邻的时间帧中的训练样本具有很强的相关性。新获得的状态序列对(h,$x^\ast$)被添加到重放内存中，若内存已满则替换最久的状态位置对。随后从存储器中随机抽样以改善DNN。过使用ADAM优化器[25]，减少了交叉熵损失。
利用经验回放机制，构建了DNN的动态训练数据集。
由于采用了随机抽样，降低了训练样本之间的相关性，加快了收敛速度。由于存储空间有限，DNN只根据最近的经验进行更新，而卸载策略π总是适应最近的信道变化。

动态调整k

更大的KK可以带来更好的临时卸货决策和更好的长期卸货政策。然而，要在每个时间帧内选择最优的卸载位置$x^∗$，反复求解带宽分配问题($P^‘$)K次将导致较高的计算复杂度。需要去设置k来权衡性能和复杂度。

在K = N固定的情况下，绘制出每个时间段的最优卸载位置索引。如下图所示，在学习过程的最开始，最优卸载位置的索引比较大。随着卸载策略的改进，我们发现大多数最优卸载位置都是上述保序量化方法生成的第一个位置。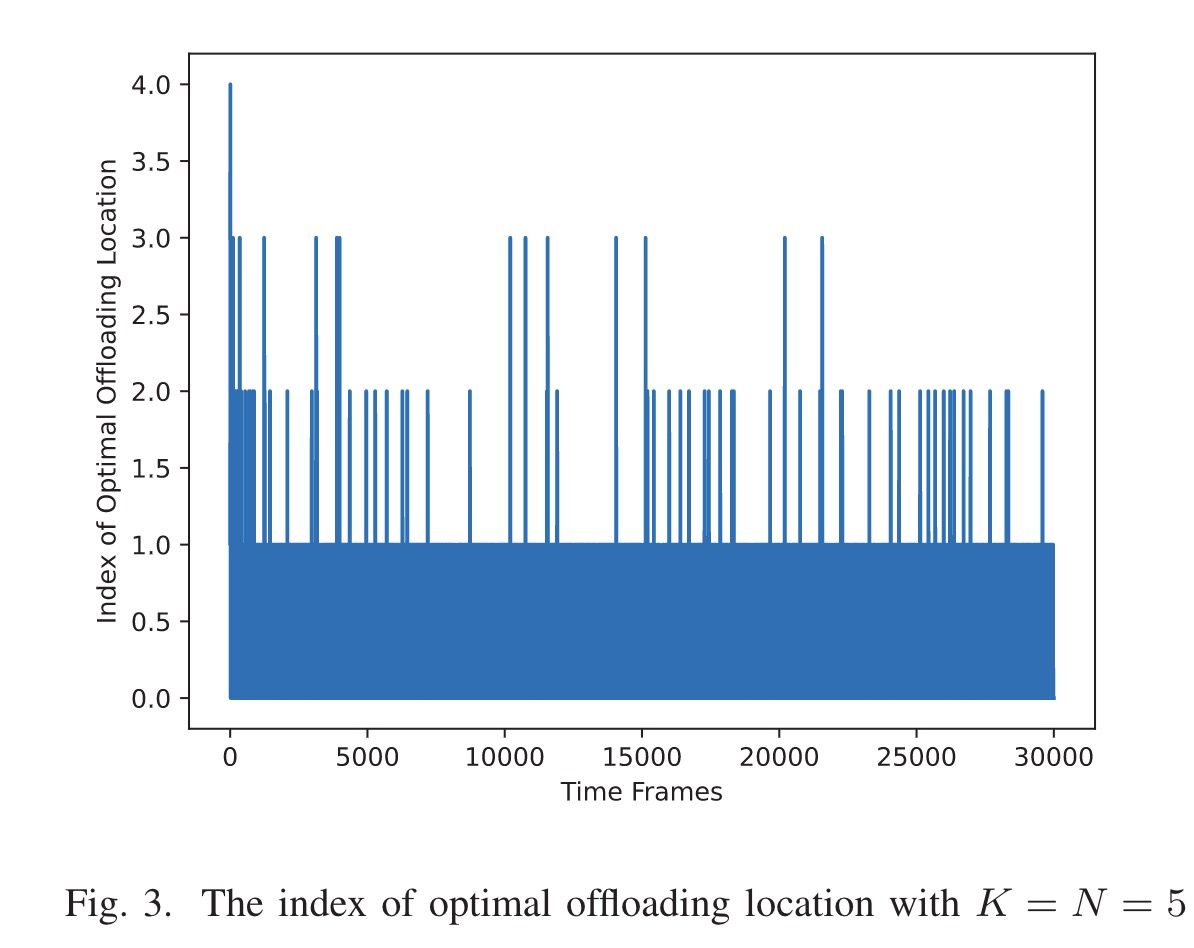

最初设置$k_1$ = N ，对于每个Δ时间范围，$K_t$将调整一次。在调整时间范围内，增加候选卸货地点的多样性。由下列式子给出

$$K_t=\{\begin{array}{ll}N& t=1\\ min(max(k_{t-1}^{\ast },\dots ,k_{t-\mathrm{\Delta }}^{\ast })+1,N)& tmod\mathrm{\Delta }=0\\ K_{t-1}& \text{ otherwise }\end{array}$$

仿真结果

对比算法：

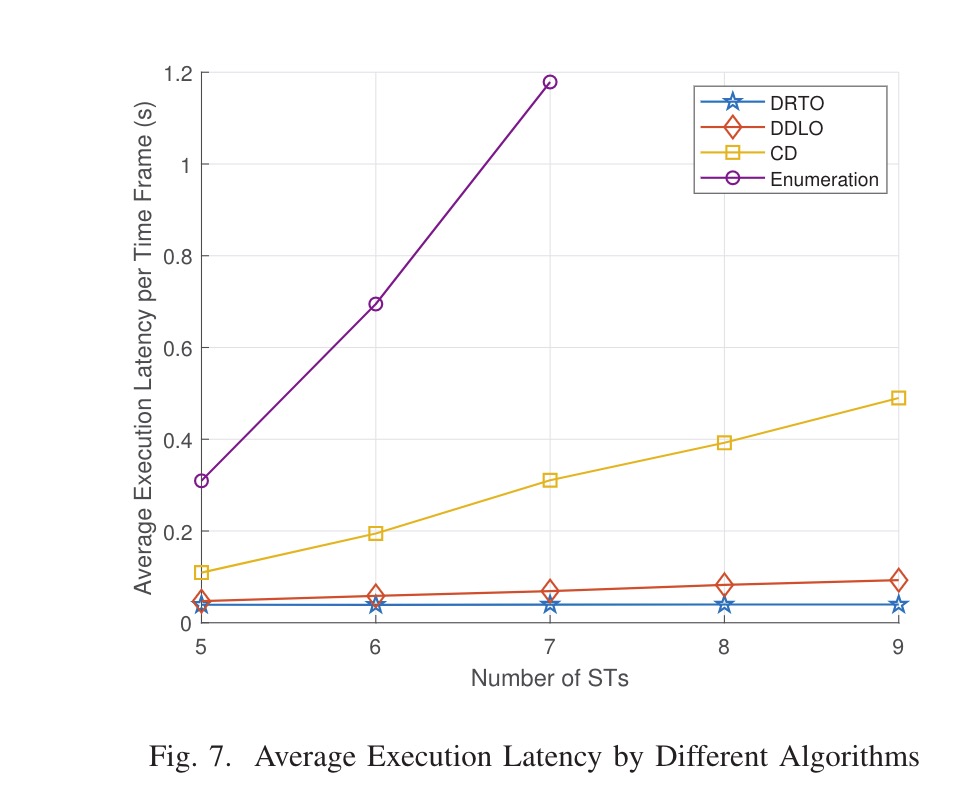
• 基于深度学习的分布式卸载(DDLO)[2]。多个DNN将重复的信道增益作为输入，每个DNN产生一个候选卸载位置。然后，根据最小卸货成本选择最优卸货地点。在与DRTO的比较中，我们假设DDLO是由NDNN组成的。
• 坐标下降(CD)[3]。CD算法是一种传统的数值优化方法，它迭代地交换每个STS的卸载位置，从而导致最大的卸载成本降低。当不能通过交换卸货位置进一步降低卸货成本时，迭代停止。
• 枚举。我们列举所有2N卸载位置组合，并贪婪地选择最佳组合。
• 纯TC计算。LEO接入卫星将所有任务转发给TC执行。
• 纯SATEC计算。LEO Access卫星在本地执行所有任务

原文链接与参考文献

Deep Reinforcement Learning-based TaskOffloading in Satellite-Terrestrial Edge ComputingNetworks

[1].Huang, Liang, Suzhi Bi, and Ying-Jun Angela Zhang. “Deep reinforcement learning for online computation offloading in wireless powered mobile-edge computing networks.” IEEE Transactions on Mobile Computing 19.11 (2019): 2581-2593.

[2].L. Huang, X. Feng, A. Feng, Y. Huang, and L. P. Qian, “Distributeddeep learning-based offloading for mobile edge computing networks,”Mobile Networks and Applications, 2018.

[3].S. Bi and Y. J. Zhang, “Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading,”IEEE TWC, 2018.